Next: 演習問題5.1 Up: ラプラス変換(The Laplace transformation) Previous: ラプラス変換(The Laplace transformation) 目次 索引
変換の一般的な考え方は何らかな一意性をもつ2つの関数の組を作ることといえます.たとえば,関数とその導関数の組を考えます.このとき,導関数は演算子,または変換と言われ,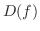 で表わします.この組は一意性をもっています.なぜなら同じ導関数をもつ2つの関数は定数を除いて等しいということができます.同様に,関数の積分,
で表わします.この組は一意性をもっています.なぜなら同じ導関数をもつ2つの関数は定数を除いて等しいということができます.同様に,関数の積分,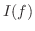 も変換です.ここで,
も変換です.ここで,
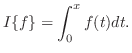
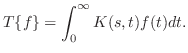
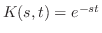 とおいたものです.
とおいたものです.
|
定義 5..1
関数 のラプラス変換は,次の積分が存在する場合,関数 のラプラス変換は,次の積分が存在する場合,関数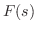 で与えられる. で与えられる.
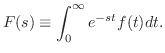
|
記号
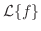 または
または
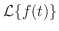 も
も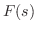 の代りに用いられます.
の代りに用いられます.
一般に変数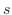 は複素数ですが,この章では
は複素数ですが,この章では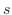 は実数とします.
は実数とします.
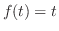 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
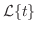 |
 |
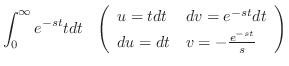 |
|
 |
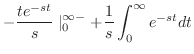 |
||
 |
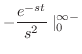 |
||
 |
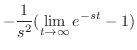 |
||
 |
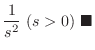 |
この例題は与えられた関数のラプラス変換が,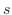 の値がある定数
の値がある定数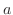 より大きいところでしか定義されない例として典型的です.ここで大事なことは定数
より大きいところでしか定義されない例として典型的です.ここで大事なことは定数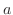 が何であるかではなく広義積分が存在するような定義域
が何であるかではなく広義積分が存在するような定義域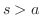 が存在するということです.後に逆変換を考えるとき,このような定義域についてもっと注意をはらいます.
が存在するということです.後に逆変換を考えるとき,このような定義域についてもっと注意をはらいます.
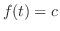 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
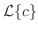 |
 |
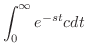 |
|
 |
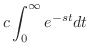 |
||
 |
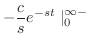 |
||
 |
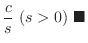 |
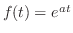 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
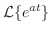 |
 |
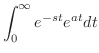 |
|
 |
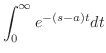 |
||
 |
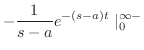 |
||
 |
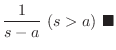 |
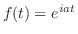 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
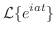 |
 |
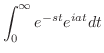 |
|
 |
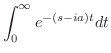 |
||
 |
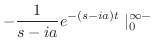 |
||
 |
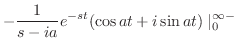 |
||
 |
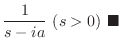 |
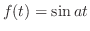 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
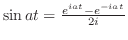 より
より
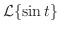 |
 |
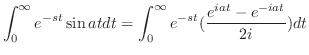 |
|
 |
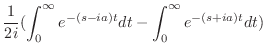 |
||
 |
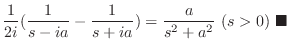 |
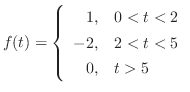
解
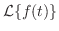 |
 |
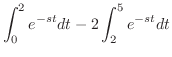 |
|
 |
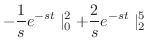 |
||
 |
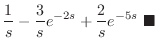 |
このような区分的に連続な関数を扱うのに便利なものとして単位ステップ関数とよばれるものがあります.単位ステップ関数(unit step function)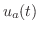 は次のように定義されます.
は次のように定義されます.
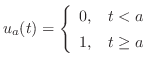
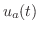 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
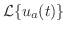 |
 |
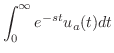 |
|
 |
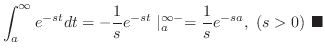 |
単位ステップ関数を用いると例題5.1の は次のように表わせます.各自考えてみて下さい.
は次のように表わせます.各自考えてみて下さい.
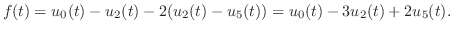
ここでこれから必要となるラプラス変換を表にまとめておきます.