Next: 演習問題3.3 Up: 連立線形微分方程式(systems of linear differential Previous: 演習問題3.2 目次 索引
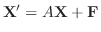 の解法を考える前に,もう一度,同次方程式の解を整理してみます.
の解法を考える前に,もう一度,同次方程式の解を整理してみます.
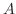 を
を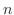 次の正方行列とします.
次の正方行列とします.
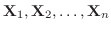 が
が
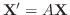 の一次独立な解のとき,
の一次独立な解のとき,
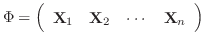
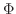 は次のような性質をもっていることが確かめられます.
は次のような性質をもっていることが確かめられます.
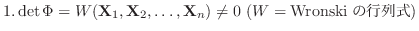
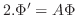
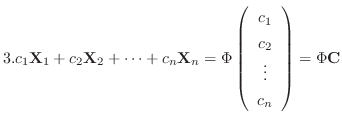
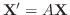 の解は
の解は
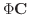 で与えられるので,前の章で学んだ定数変化法を用いて,非同次方程式
で与えられるので,前の章で学んだ定数変化法を用いて,非同次方程式
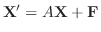 の解を
の解を
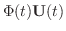 と置いてみます.行列の導関数はそれぞれの成分の導関数で与えられるので,
と置いてみます.行列の導関数はそれぞれの成分の導関数で与えられるので,
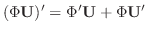
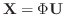 を
を
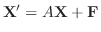 に代入すると,
に代入すると,
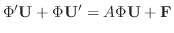
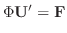
![$\displaystyle {\bf U}^{\prime} = \frac{[\Phi:{\bf F}]}{\vert\Phi\vert} $](img989.png)
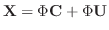
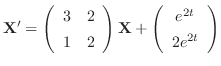 を解け.
を解け.
解
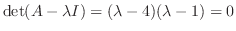 より,固有値
より,固有値
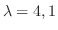 .固有値
.固有値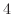 に対する固有ベクトルは
に対する固有ベクトルは
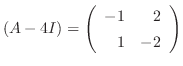 より,
より,
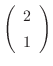 .したがって
.したがって
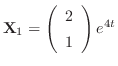 は解である.また固有値
は解である.また固有値 に対する固有ベクトルは
に対する固有ベクトルは
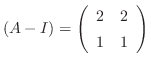 より,
より,
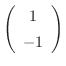 である.したがって,
である.したがって,
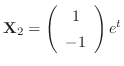 も解である.これより基本行列
も解である.これより基本行列
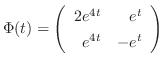
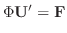
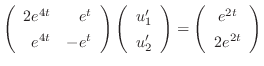
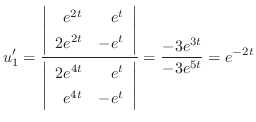
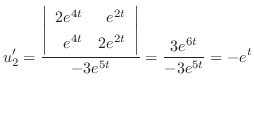
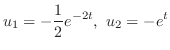
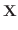 |
 |
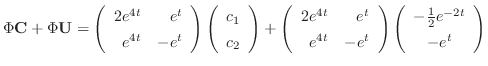 |
|
 |
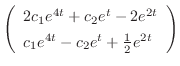 |

例題3.3は演算子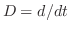 を用いることにより,求めることもできます.この方法は消去法または演算子法とよばれています.
を用いることにより,求めることもできます.この方法は消去法または演算子法とよばれています.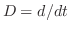 より
より
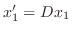 .
よって
.
よって
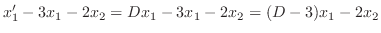
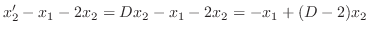
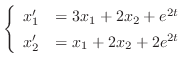
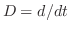 を用いることにより次のように書き直せます.
を用いることにより次のように書き直せます.
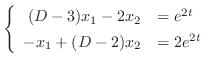 |
(3.1) |
解
ここで連立方程式を消去法で解くように,まず第1式に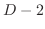 を掛け第2式に2を掛けて加えると
を掛け第2式に2を掛けて加えると
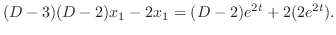
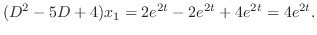 |
(3.2) |
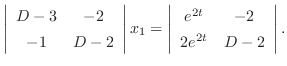
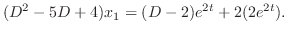
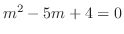 .したがって
.したがって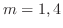 となり,
となり,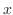 の余関数
の余関数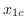 は
は
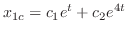
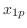 を未定係数法を用いて求める.
を未定係数法を用いて求める.
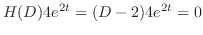
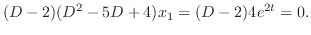
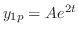 となる.これを(3.2)に代入すると
となる.これを(3.2)に代入すると
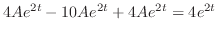
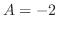 を得る.これより
を得る.これより
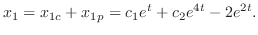
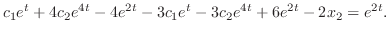
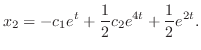

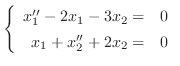 を解け.
を解け.
解
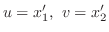 とおくと,
とおくと,
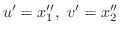 .よって与えられた微分方程式は次のように書き直せる.
.よって与えられた微分方程式は次のように書き直せる.
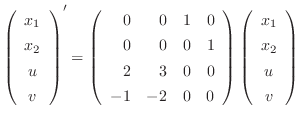
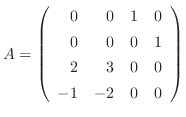 の特性方程式は
の特性方程式は
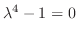 より,固有値
より,固有値
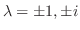 が求まる.次に固有ベクトルを求めるのだが,行列の次数が大きいので,コンピュータの力を借りる.ここではMathematicaを使用して,固有ベクトルを求めた.
が求まる.次に固有ベクトルを求めるのだが,行列の次数が大きいので,コンピュータの力を借りる.ここではMathematicaを使用して,固有ベクトルを求めた.
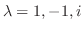 に対応する固有ベクトルは順に
に対応する固有ベクトルは順に
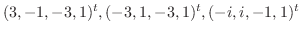
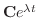 は
は
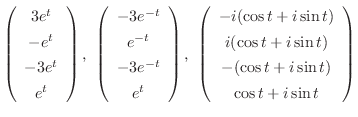
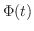 は
は
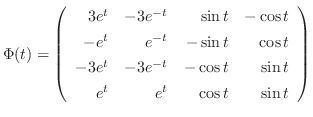
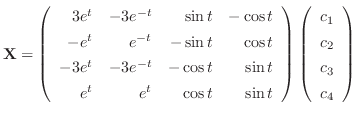
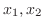 について解くと,
について解くと,
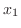 |
 |
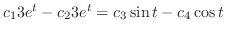 |
|
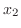 |
 |
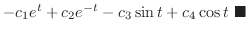 |