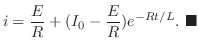Next: 演習問題1.6 Up: 1階微分方程式(1st order linear differential Previous: 演習問題1.5 目次 索引
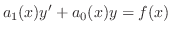
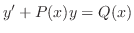
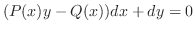
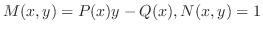 より
より
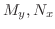 を求めると
を求めると
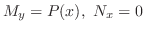
![$(1/N)[M_{y} - N_{x}] = P(x)$](img300.png) は
は だけの関数です.
そこで前節で学んだように積分因子を求めると
だけの関数です.
そこで前節で学んだように積分因子を求めると
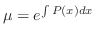
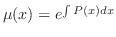 を標準形
を標準形
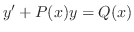 にかけると
にかけると
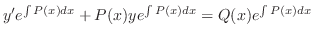
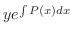 の導関数より
の導関数より
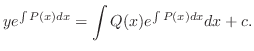
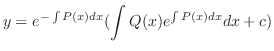
1階線形微分方程式の解は上に示した公式で求められますが,この公式から解を求めるのはあまり推薦できません.それよりも,次の例題で示すように積分因子が
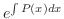 であることを使って解を求めるほうがよいでしょう.
であることを使って解を求めるほうがよいでしょう.
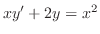 を解け.
を解け.
解 この方程式は1階の線形です.標準形に直すと
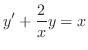
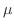 は
は
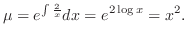
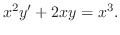
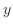 の導関数なので
の導関数なので
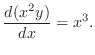
 で積分すると
で積分すると
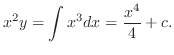
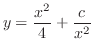

次の例題はKirchhoffの第2法則(Kirchhoff's 2nd law)を用いて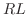 回路とよばれている電気回路を流れる電流を求めます.そこで復習.
回路とよばれている電気回路を流れる電流を求めます.そこで復習.
電気抵抗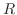 オーム,インダクタンス
オーム,インダクタンス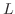 ヘンリー,容量
ヘンリー,容量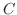 ファラデー,起電力
ファラデー,起電力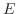 ボルトの電気回路に
ボルトの電気回路に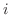 アンペアの電流を流したとき,抵抗素子,コイル,コンデンサーを通るときの電圧降下は
アンペアの電流を流したとき,抵抗素子,コイル,コンデンサーを通るときの電圧降下は
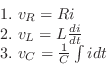 で与えられます.またKirchhoffの第2法則とはひとつの網目に沿った電圧の降下の総和と,電圧の上昇の総和は等しいことです.よって
で与えられます.またKirchhoffの第2法則とはひとつの網目に沿った電圧の降下の総和と,電圧の上昇の総和は等しいことです.よって
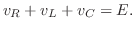
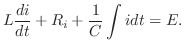
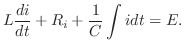
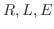 が定数,
が定数,
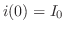 の
の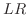 回路に流れる電流を求めよ.
回路に流れる電流を求めよ.
解 Kirchhoffの第2法則より
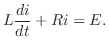
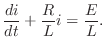
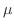 は
は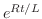 となる.積分因子を標準形にかけて整理すると
となる.積分因子を標準形にかけて整理すると
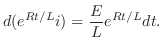
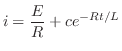
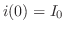 より
より
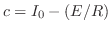 .
よって
.
よって