Next: 2.2 解答 Up: 演習問題解答 Previous: 1.8 解答 索引
2.1
1.
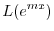 |
 |
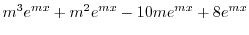 |
|
 |
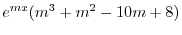 |
||
 |
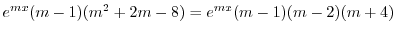 |
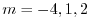 のとき,
のとき,
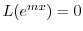 となる.よって
となる.よって
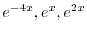 は解であり一般解は
は解であり一般解は
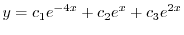
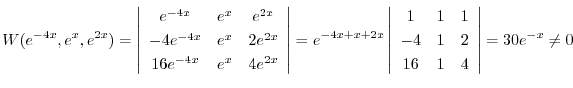

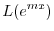 |
 |
 |
|
 |
 |
||
 |
 |
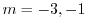 のとき,
のとき,
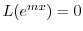 となる.よって
となる.よって
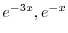 は解であり一般解は
は解であり一般解は
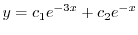
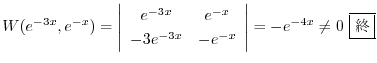
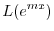 |
 |
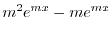 |
|
 |
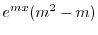 |
||
 |
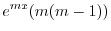 |
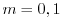 のとき,
のとき,
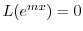 となる.よって
となる.よって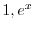 は解であり一般解は
は解であり一般解は
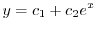
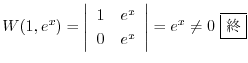
 |
 |
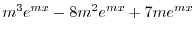 |
|
 |
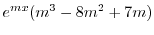 |
||
 |
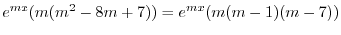 |
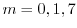 のとき,
のとき,
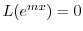 となる.よって
となる.よって
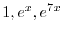 は解であり一般解は
は解であり一般解は
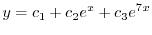
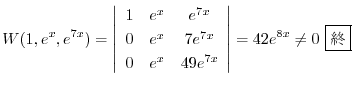
2.
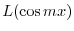 |
 |
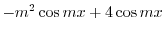 |
|
 |
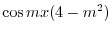 |
||
 |
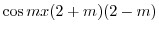 |
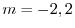 のとき,
のとき,
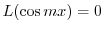 となる.よって
となる.よって
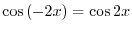 は解である.また
は解である.また
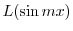 |
 |
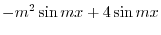 |
|
 |
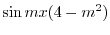 |
||
 |
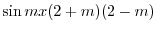 |
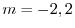 のとき,
のとき,
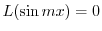 となる.よって
となる.よって
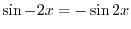 は解である.ここで
は解である.ここで 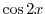 と
と 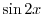 は
は
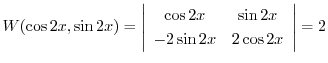
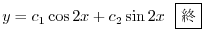
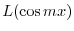 |
 |
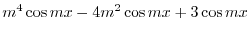 |
|
 |
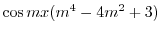 |
||
 |
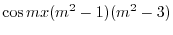 |
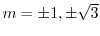 のとき,
のとき,
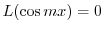 となる.よって
となる.よって
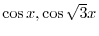 は解である.また
は解である.また
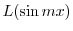 |
 |
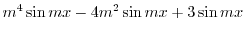 |
|
 |
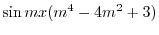 |
||
 |
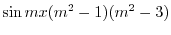 |
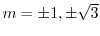 のとき,
のとき,
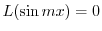 となる.よって
となる.よって
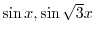 は解である.ここで
は解である.ここで
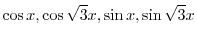
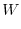 |
 |
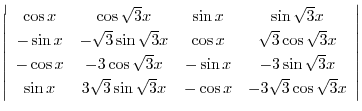 |
|
 |
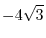 |
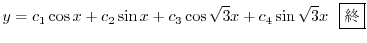
3.
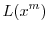 |
 |
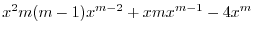 |
|
 |
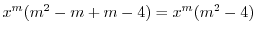 |
||
 |
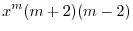 |
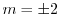 のとき,
のとき,
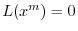 となる.よって
となる.よって
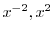 は解である.
ここで
は解である.
ここで
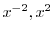 は
は
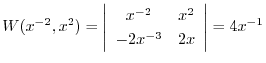
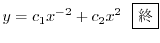
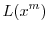 |
 |
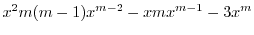 |
|
 |
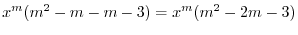 |
||
 |
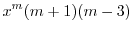 |
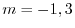 のとき,
のとき,
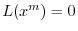 となる.よって
となる.よって
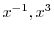 は解である.
ここで
は解である.
ここで
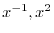 は
は