Next: 索引 Up: 演習問題解答 Previous: 8.1 解答 索引
8.2
![$\displaystyle {\cal F}_{s}[u_{xx}]$](img2961.png) |
 |
![$\displaystyle - \omega {\cal F}_{c}[u_{x}]$](img2962.png) |
|
 |
![$\displaystyle - \omega[-u(0,t) + \omega {\cal F}_{s}[u]]$](img2963.png) |
||
 |
![$\displaystyle -\omega^2 {\cal F}_{s}[u] = - \omega^2 U_{s}(\omega,t)$](img2964.png) |
![$\displaystyle {\cal F}_{s}[u_{t}] = \frac{\partial}{\partial t}{\cal F}_{s}[u] = \frac{\partial}{\partial t}U_{s}(\omega ,t) $](img2965.png)
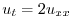 の両辺にフーリエ変換を施すと
の両辺にフーリエ変換を施すと
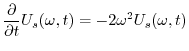
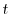 について1階線形なので,
について1階線形なので,
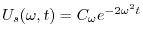
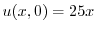 を用いると
を用いると
![$\displaystyle {\cal F}_{s}[u(x,0)] = U_{s}(\omega,0) = C_{\omega} $](img2970.png)
![$\displaystyle {\cal F}_{s}[u(x,0)]$](img2971.png) |
 |
![$\displaystyle {\cal F}_{s}[25x] = \frac{2}{\pi}\int_{0}^{4}25x \sin{\omega x}dx$](img2972.png) |
|
 |
![$\displaystyle \frac{50}{\pi}\left\{\left[\frac{-x\cos{\omega x}}{\omega} \right]_{0}^{4} + \frac{1}{\omega}\int_{0}^{4} \cos{\omega x} dx \right\}$](img2973.png) |
||
 |
![$\displaystyle \frac{50}{\pi}\left\{\frac{-4 \cos{4 \omega}}{\omega} + \left[\frac{\sin{\omega x}}{\omega^2}\right]_{0}^{4}\right\}$](img2974.png) |
||
 |
![$\displaystyle \frac{50}{\pi}\left[\frac{-4\cos{4 \omega}}{\omega} + \frac{\sin{4 \omega x}}{\omega^2} \right]$](img2975.png) |
![$\displaystyle U_{s}(\omega,t) = \frac{50}{\pi}\left[\frac{-4\omega \cos{4\omega} + \sin{4\omega}}{\omega^2}\right] e^{-2\omega^2 t} $](img2976.png)
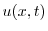 |
 |
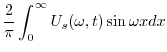 |
|
 |
![$\displaystyle \frac{2}{\pi}\int_{0}^{\infty}\frac{50}{\pi}\left[\frac{-4\omega ...
...omega} + \sin{4\omega}}{\omega^2}\right] e^{-2\omega^2 t}\sin{\omega x} d\omega$](img2978.png) |
||
 |
![$\displaystyle \frac{100}{\pi^2} \int_{0}^{\infty}\left[\frac{-4\omega \cos{4\omega} + \sin{4\omega}}{\omega^2}\right] e^{-2\omega^2 t}\sin{\omega x} d \omega$](img2979.png) |
![$\displaystyle {\cal F}[u_{tt}] = \frac{\partial^2}{\partial t^2}U(\omega,t) $](img2980.png)
![$\displaystyle {\cal F}[u_{xx}] = (i \omega^2)U(\omega,t)= - \omega^2 U(\omega,t) $](img2981.png)
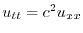 は次の常微分方程式に変換される.
は次の常微分方程式に変換される.
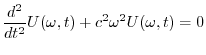
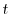 について線形で,特性根は
について線形で,特性根は
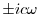 なので
なので
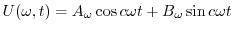
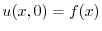 より
より
![$\displaystyle {\cal F}[u(x,0)] = U(\omega,0) = F(\omega) = A_{\omega} $](img2986.png)
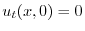 より
より
![$\displaystyle {\cal F}[u_{t}(x,0)] = \frac{\partial}{\partial t}U(\omega,0) = c\omega B_{\omega} = 0$](img2987.png)
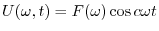
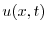 を求めると,
を求めると,
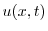 |
 |
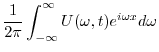 |
|
 |
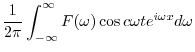 |
||
 |
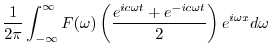 |
||
 |
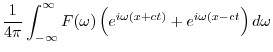 |
||
 |
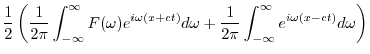 |
||
 |
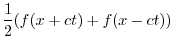 |
![$\displaystyle {\cal F}_{c}[u_{xx}]$](img2995.png) |
 |
![$\displaystyle - u_{x}(0,t) + \omega {\cal F}_{s}[u_{x}]$](img2996.png) |
|
 |
![$\displaystyle - f(t) - \omega^2 {\cal F}_{c}[u] = -f(t) - \omega^2 U_{c}(\omega,t)$](img2997.png) |
![$\displaystyle {\cal F}_{c}[u_{tt}] = \frac{\partial^2}{\partial t^2}U_{c}(\omega,t) $](img2998.png)
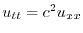 の両辺にフーリエ変換を施すと
の両辺にフーリエ変換を施すと
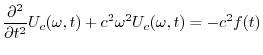
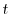 について1階線形なので,余関数は
について1階線形なので,余関数は
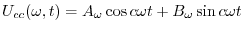
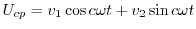
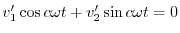
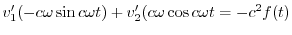
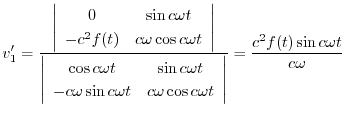
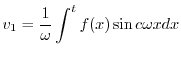
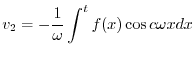
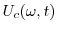 |
 |
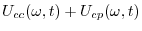 |
|
 |
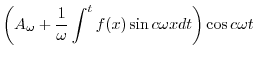 |
||
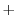 |
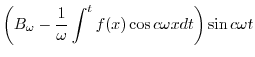 |
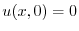 より
より
![$\displaystyle {\cal F}_{c}[u(x,0)] = U_{c}(\omega,0) = A_{\omega} = 0 $](img3011.png)
![$\displaystyle {\cal F}_{c}[u_{t}(x,0)] = \frac{\partial}{\partial t}U_{c}(\omega,0) = -\frac{1}{\omega} f(0) + c\omega B_{\omega} = 0 $](img3012.png)
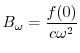
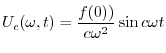
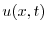 を求めると,
を求めると,
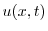 |
 |
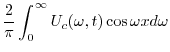 |
|
 |
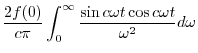 |