Next: 5.1 解答 Up: 演習問題解答 Previous: 4.2 解答 索引
4.3
1.
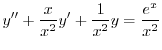
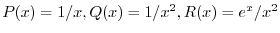 .これより
.これより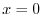 は特異点.次に
は特異点.次に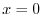 が確定特異点か不確定特異点を調べる.
が確定特異点か不確定特異点を調べる.
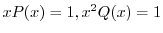 より
より
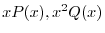 は
は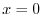 で共に解析的.よって
で共に解析的.よって
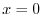 は確定特異点.
は確定特異点.

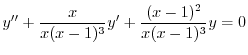
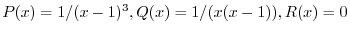 .これより
.これより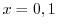 は特異点.次に
は特異点.次に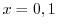 が確定特異点か不確定特異点を調べる.
が確定特異点か不確定特異点を調べる.
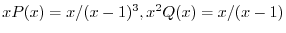 より
より
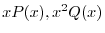 は
は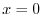 で共に解析的.よって
で共に解析的.よって
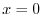 は確定特異点.次に
は確定特異点.次に
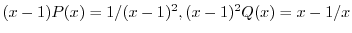 より
より
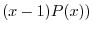 は
は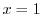 で解析的でない.よって
で解析的でない.よって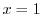 は不確定特異点.
は不確定特異点.

(c) 標準形に直すと
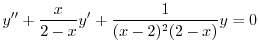
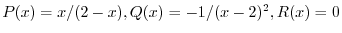 .これより
.これより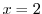 は特異点.次に
は特異点.次に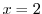 が確定特異点か不確定特異点を調べる.
が確定特異点か不確定特異点を調べる.
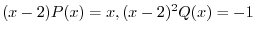 より
より
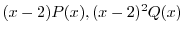 は
は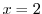 で共に解析的.よって
で共に解析的.よって
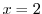 は確定特異点.
は確定特異点.

2.
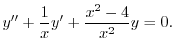
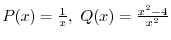 .よって
.よって
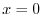 は確定特異点.そこで解を
は確定特異点.そこで解を
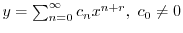 とおく.これを微分することにより得られる
とおく.これを微分することにより得られる
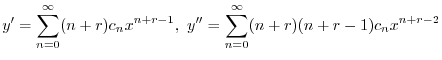
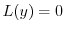 に代入すると
に代入すると
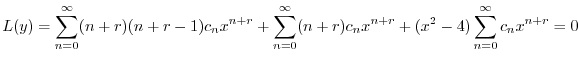
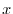 のベキを必ず一番小さいものにそろえると
のベキを必ず一番小さいものにそろえると
![$\displaystyle \underbrace{(r^2 -4)c_{0}x^{r}}_{n = 0} + \underbrace{((r+1)^2 -4...
...x^{r+1}}_{n = 1} + \sum_{n=2}^{\infty}[((n+r)^2 - 4)c_{n} + c_{n-2}]x^{n+r} = 0$](img1916.png) |
 を解くと
を解くと となる.
となる.
ここで のときの解を求める.右辺は恒等的に零なので,左辺の
のときの解を求める.右辺は恒等的に零なので,左辺の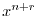 の係数は零である.よって
の係数は零である.よって
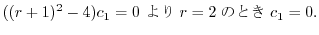
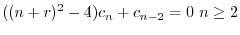
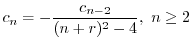
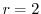 とおくと
とおくと
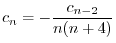
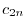 |
 |
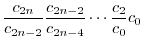 |
|
 |
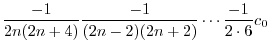 |
||
 |
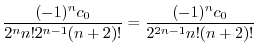 |
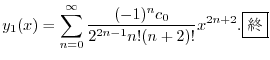
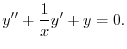
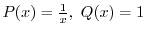 .よって
.よって
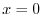 は確定特異点.そこで解を
は確定特異点.そこで解を
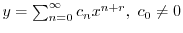 とおく.これを微分することにより得られる
とおく.これを微分することにより得られる
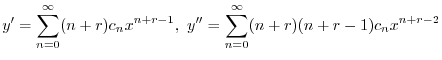
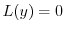 に代入すると
に代入すると
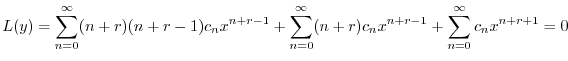
 のベキを一番小さいものにそろえると
のベキを一番小さいものにそろえると
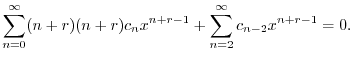
![$\displaystyle \underbrace{r^{2}c_{0}x^{r-1}}_{n = 0} + \underbrace{(r+1)^2 c_{1}x^{r}}_{n = 1} + \sum_{n=2}^{\infty}[(n+r)(n+r) c_{n} + c_{n-2}]x^{n+r-1} = 0$](img1934.png) |
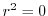 を解くと
を解くと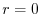 となる.
となる.
ここで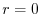 のときの解を求める.右辺は恒等的に零なので,左辺の
のときの解を求める.右辺は恒等的に零なので,左辺の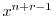 の係数は零である.よって
の係数は零である.よって
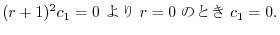
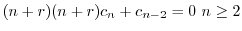
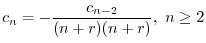
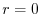 とおくと
とおくと
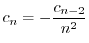
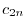 |
 |
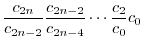 |
|
 |
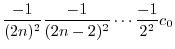 |
||
 |
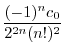 |
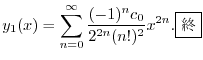
(c)
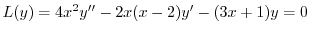 を標準形に直すと
を標準形に直すと
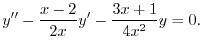
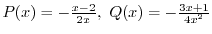 .よって
.よって
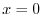 は確定特異点.そこで解を
は確定特異点.そこで解を
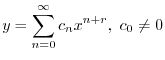
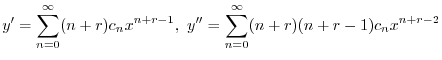
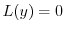 に代入すると
に代入すると
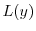 |
 |
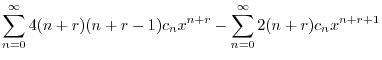 |
|
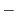 |
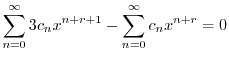 |
 のベキを一番小さいものにそろえると
のベキを一番小さいものにそろえると
![$\displaystyle \sum_{n=0}^{\infty}[4(n+r)(n+r) - 1]c_{n}x^{n+r} - \sum_{n=1}^{\infty}[2(n+r-1) + 3]c_{n-1}x^{n+r} = 0 .$](img1952.png)
![$\displaystyle \underbrace{(4r^{2}-1)c_{0}x^{r}}_{n = 0} + \sum_{n=1}^{\infty}[(4(n+r)^2-1) c_{n} - (2(n+r-1)+3) c_{n-1}]x^{n+r} = 0$](img1953.png) |
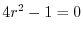 を解くと
を解くと
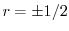 となる.
となる.
ここで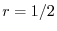 のときの解を求める.右辺は恒等的に零なので,左辺の
のときの解を求める.右辺は恒等的に零なので,左辺の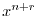 の係数は零である.よって
の係数は零である.よって
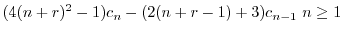
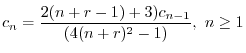
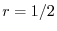 とおくと
とおくと
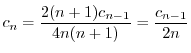
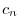 |
 |
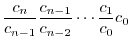 |
|
 |
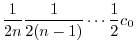 |
||
 |
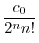 |
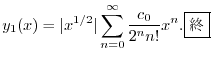
3.
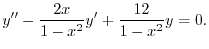
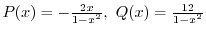 .よって
.よって
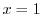 は確定特異点.そこで
は確定特異点.そこで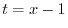 とおくと,
とおくと,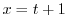 より
より
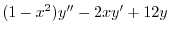 |
|||
 |
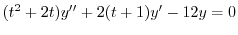 |
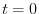 は確定特異点となるので,解を
は確定特異点となるので,解を
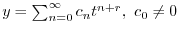 とおく.これを微分することにより得られる
とおく.これを微分することにより得られる
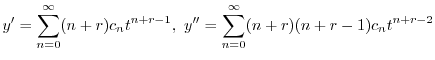
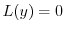 に代入すると
に代入すると
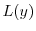 |
 |
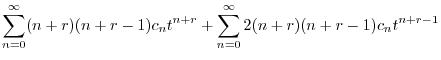 |
|
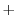 |
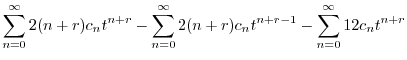 |
||
 |
![$\displaystyle \sum_{n=0}^{\infty}[(n+r)(n+r+1) - 12]c_{n}t^{n+r} + \sum_{n=0}^{\infty}[2(n+r)^2 c_{n}]t^{n+r-1} = 0$](img1976.png) |
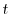 のベキを一番小さいものにそろえると
のベキを一番小さいものにそろえると
![$\displaystyle \sum_{n=1}^{\infty}[(n+r-1)(n+r) - 12]c_{n-1}t^{n+r} + \sum_{n=0}^{\infty}2(n+r)^2 c_{n}t^{n+r-1} $](img1977.png)
![$\displaystyle L(y) = 2r^2 c_{0}t^{r-1} + \sum_{n=1}^{\infty}[(n+r-1)(n+r) - 12]c_{n-1} + 2(n+r)^2 c_{n}]t^{n+r-1} = 0 $](img1978.png)
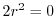 を解くと
を解くと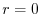 となる.
となる.
ここで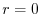 のときの解を求める.右辺は恒等的に零なので,左辺の
のときの解を求める.右辺は恒等的に零なので,左辺の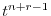 の係数は零である.よって
の係数は零である.よって
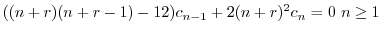
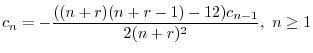
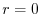 とおくと
とおくと
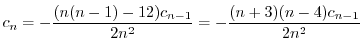
 を求めると
を求めると
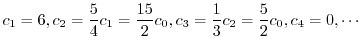
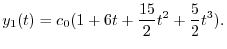
 を求める.
を求める. は階数低減法で求められる.
は階数低減法で求められる.
(階数低減法による)
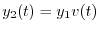 とおき
とおき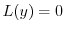 に代入すると
に代入すると
![$\displaystyle y_{1}v^{\prime\prime}(t) + [2y_{1}^{\prime} + \frac{2t+2}{t^2 +2t}y_{1}]v^{\prime}(t) = 0$](img1989.png)
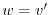 とおくと
とおくと
![$\displaystyle \frac{w^{\prime}}{w} = - [2\frac{y_{1}^{\prime}}{y_{1}} + \frac{2t+2}{t^2 +2t}]$](img1991.png)
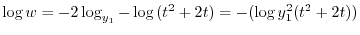
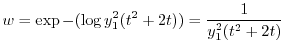
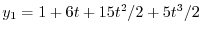 を用いると
を用いると
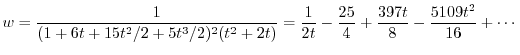
 |
 |
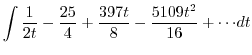 |
|
 |
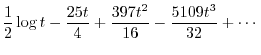 |
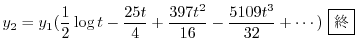
別解
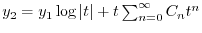 で与えられるので,これを
で与えられるので,これを
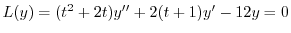 に代入し
に代入し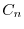 を求める.計算の都合上
を求める.計算の都合上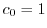 とおくと.
とおくと.
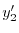 |
 |
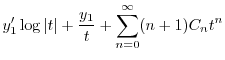 |
|
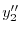 |
 |
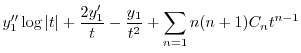 |
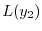 |
 |
![$\displaystyle (t^2 + 2t)[y_{1}^{\prime\prime} \log{\vert t\vert} + \frac{2y_{1}^{\prime}}{t} - \frac{y_{1}}{t^2} + \sum_{n=1}n(n+1)C_{n}t^{n-1}]$](img2009.png) |
|
 |
![$\displaystyle (2t + 2)[y_{1}^{\prime} \log{\vert t\vert} + \frac{y_{1}}{t} + \sum_{n=0}^{\infty}(n+1)C_{n}t^{n} ]$](img2010.png) |
||
 |
![$\displaystyle 12 [y_{1} \log{\vert t\vert} + t\sum_{n=0}^{\infty}C_{n}t^{n}]$](img2011.png) |
||
 |
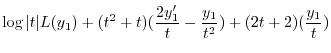 |
||
 |
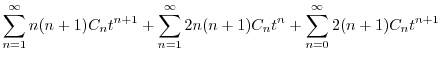 |
||
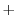 |
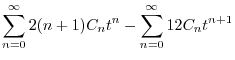 |
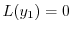 に注意し,
に注意し,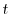 のベキを一番小さいのでそろえると
のベキを一番小さいのでそろえると
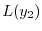 |
 |
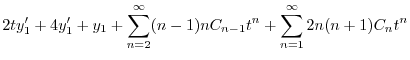 |
|
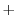 |
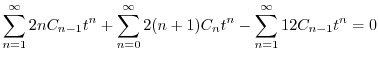 |
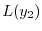 |
 |
![$\displaystyle 2ty_{1}^{\prime} + 4y_{1}^{\prime} + y_{1} +
2C_{0} + [4C_{1} + (2 - 12)C_{0}]t$](img2018.png) |
|
 |
![$\displaystyle \sum_{n=2}^{\infty}[((n+1)n - 12)C_{n-1} + (2n+2)(n+1)C_{n} ]t^{n} = 0$](img2019.png) |
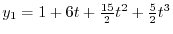 を用いると
を用いると
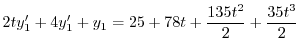
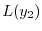 |
 |
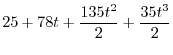 |
|
 |
![$\displaystyle 2C_{0} + [4C_{1} + (2 - 12)C_{0}]t$](img2023.png) |
||
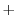 |
![$\displaystyle \sum_{n=2}^{\infty}[((n+1)n - 12)C_{n-1} + 2(n+1)^2 C_{n} ]t^{n} = 0$](img2024.png) |
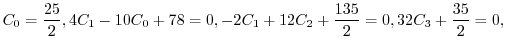
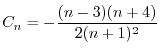
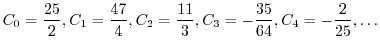
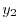 |
 |
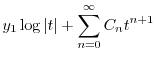 |
|
 |
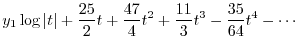 |
