Next: 4.3 解答 Up: 演習問題解答 Previous: 4.1 解答 索引
4.2
1.
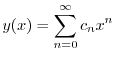
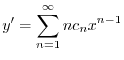
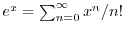 より,これらを与えられた方程式に代入すると
より,これらを与えられた方程式に代入すると
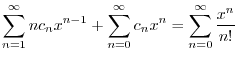
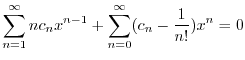
 のベキを一番小さな
のベキを一番小さな になるようにそろえると,
になるようにそろえると,
![$\displaystyle \sum_{n=1}^{\infty}[nc_{n} + c_{n-1} - \frac{1}{(n-1)!}]x^{n-1} = 0 . $](img1783.png)
 の係数はすべて0になる.よって漸化式
の係数はすべて0になる.よって漸化式
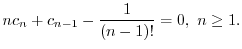
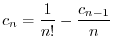
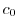 は初期条件
は初期条件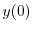 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
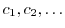 を順次求めると
を順次求めると
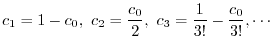
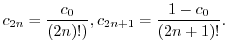
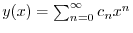 に代入すると
に代入すると
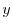 |
 |
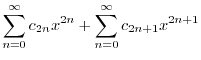 |
|
 |
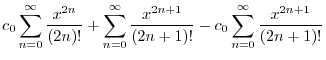 |
||
 |
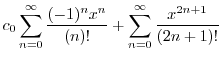 |
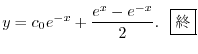
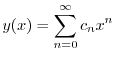
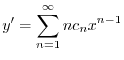
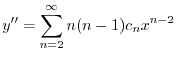
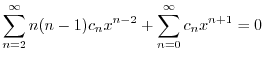
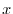 のベキを一番小さな
のベキを一番小さな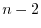 になるようにそろえると,
になるようにそろえると,
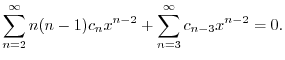
![$\displaystyle 2c_{2} + \sum_{n=3}^{\infty}[n(n-1)c_{n} + c_{n-3}]x^{n-2} = 0 $](img1802.png)
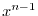 の係数はすべて0になる.よって漸化式
の係数はすべて0になる.よって漸化式
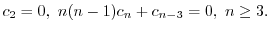
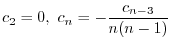
 は初期条件
は初期条件
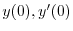 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
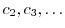 を順次求めると
を順次求めると
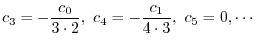
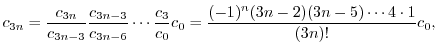
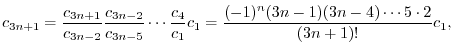
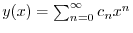 に代入すると
に代入すると
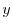 |
 |
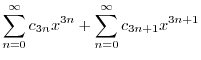 |
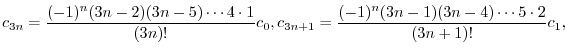

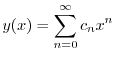
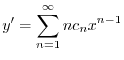
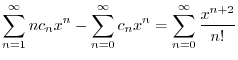
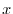 のベキを一番小さな
のベキを一番小さな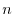 になるようにそろえると,
になるようにそろえると,
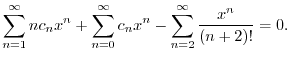
![$\displaystyle c_{1}x - c_{0} - c_{1}x + \sum_{n=2}^{\infty}[nc_{n} - c_{n} - \frac{1}{(n-2)!}]x^{n} = 0. $](img1816.png)
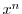 の係数はすべて0になる.よって漸化式
の係数はすべて0になる.よって漸化式
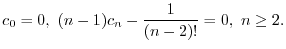
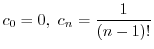
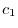 は初期条件
は初期条件
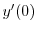 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
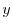 |
 |
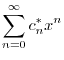 |
|
 |
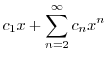 |
||
 |
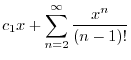 |
||
 |
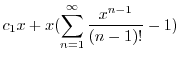 |
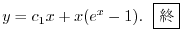
(d)
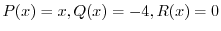 より,
より,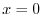 は通常点.よって,解を
は通常点.よって,解を
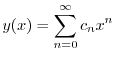
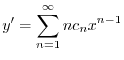
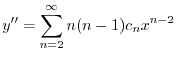
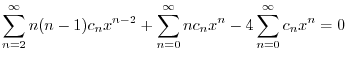
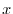 のベキを一番小さな
のベキを一番小さな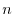 になるようにそろえると,
になるようにそろえると,
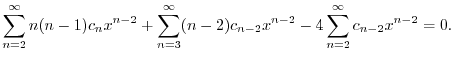
![$\displaystyle 2c_{2} - 4c_{0} + \sum_{n=3}^{\infty}[n(n-1)c_{n} + (n-6)c_{n-2}]x^{n-2} = 0. $](img1830.png)
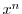 の係数はすべて0になる.よって漸化式
の係数はすべて0になる.よって漸化式
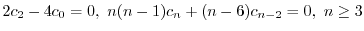
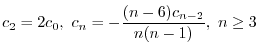
 は初期条件
は初期条件
 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
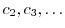 を順次求めると
を順次求めると
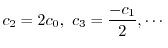
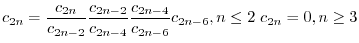
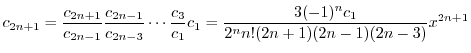
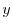 |
 |
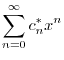 |
|
 |
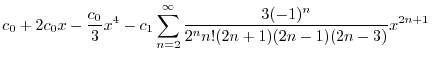 |

2.
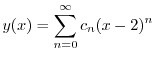
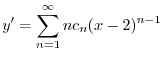
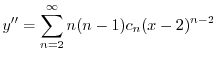
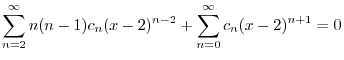
 のベキを一番小さな
のベキを一番小さな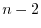 になるようにそろえると,
になるようにそろえると,
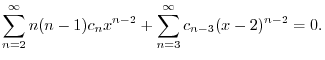
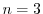 にそろえると,
にそろえると,
^{n-2} = 0. $](img1846.png)
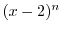 の係数はすべて0になる.よって漸化式
の係数はすべて0になる.よって漸化式
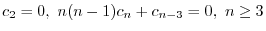
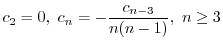
 は初期条件
は初期条件
 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
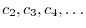 を順次求めると
を順次求めると
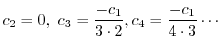
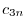 |
 |
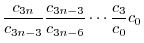 |
|
 |
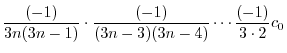 |
||
 |
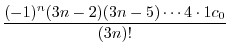 |
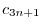 |
 |
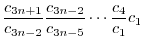 |
|
 |
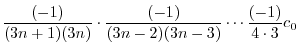 |
||
 |
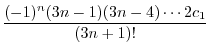 |
||
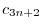 |
 |
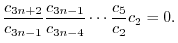 |
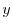 |
 |
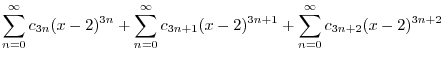 |
|
 |
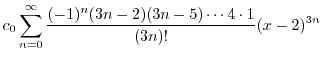 |
||
 |
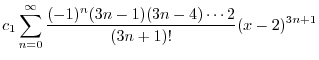 |

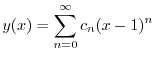
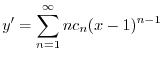
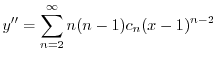
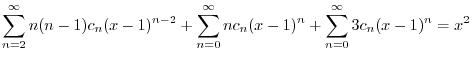
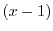 のベキを一番小さな
のベキを一番小さな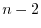 になるようにそろえると,
になるようにそろえると,
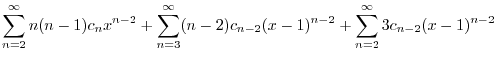 |
|||
 |
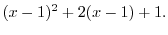 |
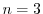 にそろえると,
にそろえると,
^{n-2} = (x-1)^2 + 2(x-1) + 1. $](img1874.png)
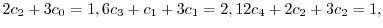
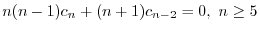
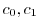 は初期条件
は初期条件
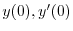 で決まるので,この場合は任意の定数と考えられる.よって,
で決まるので,この場合は任意の定数と考えられる.よって,
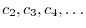 を順次求めると
を順次求めると
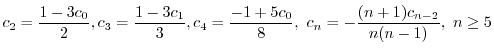
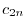 |
 |
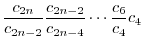 |
|
 |
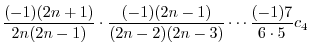 |
||
 |
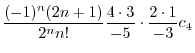 |
||
 |
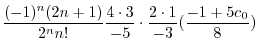 |
||
 |
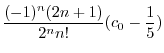 |
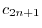 |
 |
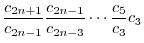 |
|
 |
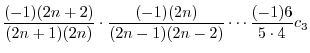 |
||
 |
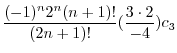 |
||
 |
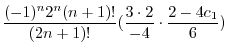 |
||
 |
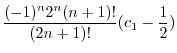 |
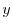 |
 |
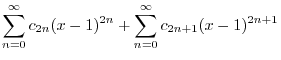 |
|
 |
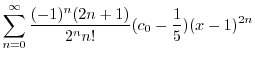 |
||
 |
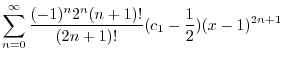 |
