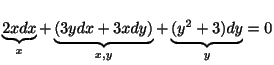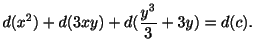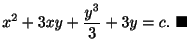: 演習問題
: 1階微分方程式
: 演習問題
目次
索引
この節では変数分離形ではないが,積分を2回行なうことによって解が得られる微分方程式について考えます.まず2変数関数の全微分を思い出してもらいます.2変数関数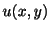 の全微分は
で与えられます.よってもし2つの偏微分
の全微分は
で与えられます.よってもし2つの偏微分
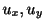 がわかれば,全微分
がわかれば,全微分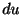 が求まります.逆に,関数の全微分がわかると次の例題が示すように,その関数を任意の定数の範囲できめることができます.
が求まります.逆に,関数の全微分がわかると次の例題が示すように,その関数を任意の定数の範囲できめることができます.
例題 1.10
ある関数
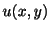
の全微分は
で与えられている.このとき,
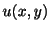
を求めよ.
解
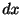 と
と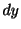 の係数は
の係数は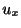 と
と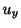 である.したがって
である.したがって
最初の式を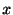 について積分すると
ここで
について積分すると
ここで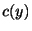 は
は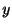 についての任意関数(なぜ?).この式を
についての任意関数(なぜ?).この式を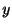 について偏微分すると
となる.この
について偏微分すると
となる.この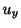 と最初に与えられた
と最初に与えられた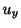 は等しいはずであるから,
これより
は等しいはずであるから,
これより
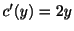 となり,
となり,
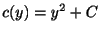 を得る.ただし
を得る.ただし は任意定数.よって
である.
は任意定数.よって
である.
次の定義は全微分と完全微分形微分方程式を結びつけてくれます.
例題 1.11
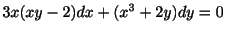
を解け.
解
例題1.10で上の微分方程式の左辺が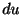 と等しい関数
と等しい関数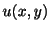 を求めた.よって一般解は
を求めた.よって一般解は
次の定理は与えられた微分方程式が完全微分形か,でないか簡単にテストする方法を示唆しています.
証明
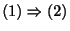
微分方程式が完全微分形ならば,
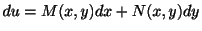 となる関数
となる関数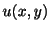 が存在する.よって
が存在する.よって
を得る.次に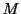 を
を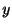 で偏微分,
で偏微分,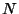 を
を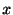 で偏微分すると
となる.ここで
で偏微分すると
となる.ここで
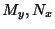 は仮定より連続なので
は仮定より連続なので
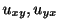 も連続である.よって微積分学で学んだSchwartzの定理(Schwarz lemma)より
も連続である.よって微積分学で学んだSchwartzの定理(Schwarz lemma)より
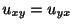 となり,
となり,
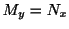 を得る.
を得る.
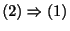
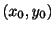 を
を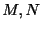 の定義域に属する点とする.
まず,
の定義域に属する点とする.
まず,
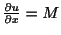 より
を得る. これが
より
を得る. これが
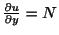 を満たすように,つまり
が成り立つように
を満たすように,つまり
が成り立つように
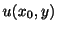 を定めればよい.
を定めればよい.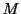 は連続な偏導関数をもつから,微分と積分の順序の交換ができて
が成り立つ.ここで
は連続な偏導関数をもつから,微分と積分の順序の交換ができて
が成り立つ.ここで
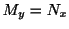 より
より
を得る.したがって,
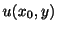 は
を満たさなければならない.そこで
は
を満たさなければならない.そこで
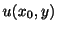 を
と定めると
これより
となり,
を
と定めると
これより
となり,
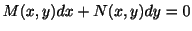 は完全微分形である.
は完全微分形である.
この定理の証明の中に完全微分形のときの解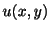 が与えられています.つまり
が与えられています.つまり
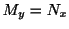 のとき,一般解は
のとき,一般解は
で与えられます.
例題 1.12
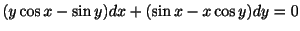
を解け.
解
より方程式は完全微分形である.そこで
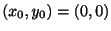 として一般解を求めると
として一般解を求めると
となり,一般解は
例題 1.13
初期値問題
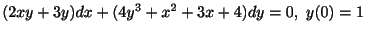
を解け.
解
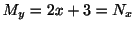 より,方程式は完全微分形である.よって
より,方程式は完全微分形である.よって
これより,一般解
を得る.最後に初期条件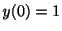 より
より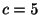 が定まる.
が定まる.
公式
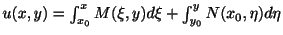 を用いて,一般解を求める方法の他に,もっとよく用いられている方法にくくり直し法(grouping method)とよばれているものがあります.この方法を次の例題を用いて説明します.
を用いて,一般解を求める方法の他に,もっとよく用いられている方法にくくり直し法(grouping method)とよばれているものがあります.この方法を次の例題を用いて説明します.
例題 1.14
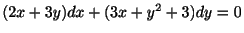
を解け.
解
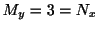 より,方程式は完全微分形である.そこで
より,方程式は完全微分形である.そこで
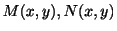 を
を
となるようにくくり直す.次に全微分を用いて書き直すと
これより,





: 演習問題
: 1階微分方程式
: 演習問題
目次
索引
Administrator
平成26年9月18日
![]() と
と![]() の係数は
の係数は![]() と
と![]() である.したがって
である.したがって
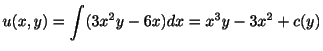
![]() と等しい関数
と等しい関数![]() を求めた.よって一般解は
を求めた.よって一般解は
![]()
![]() となる関数
となる関数![]() が存在する.よって
が存在する.よって
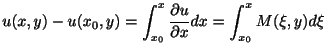
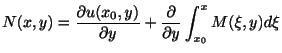
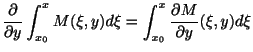
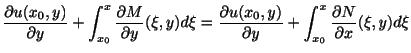
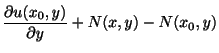
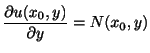
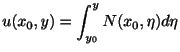
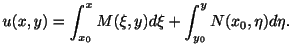
![]() が与えられています.つまり
が与えられています.つまり
![]() のとき,一般解は
のとき,一般解は
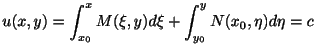
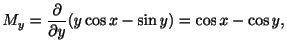
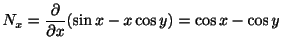
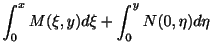
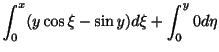
![]() より,方程式は完全微分形である.よって
より,方程式は完全微分形である.よって
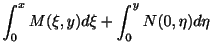
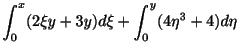
![]() を用いて,一般解を求める方法の他に,もっとよく用いられている方法にくくり直し法(grouping method)とよばれているものがあります.この方法を次の例題を用いて説明します.
を用いて,一般解を求める方法の他に,もっとよく用いられている方法にくくり直し法(grouping method)とよばれているものがあります.この方法を次の例題を用いて説明します.
![]() より,方程式は完全微分形である.そこで
より,方程式は完全微分形である.そこで
![]() を
を