




: 演習問題
: 級数による解法
: 演習問題
目次
索引
前節で2階線形微分方程式
は,通常点のまわりで整級数を用いて解を表わすことができることを学びました.ここでは,通常点以外点を考えます.通常点でない点は特異点(singular point)といいます.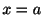 が特異点のとき,
が
が特異点のとき,
が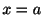 でともに解析的であるとき,
でともに解析的であるとき,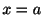 は確定特異点(regular singular point)といい,それ以外は不確定特異点(irregular singular point)といいます.
は確定特異点(regular singular point)といい,それ以外は不確定特異点(irregular singular point)といいます.
例題 4.3
次の微分方程式の特異点を見つけ,分類せよ.
解
より
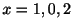 は特異点.次に
より
は特異点.次に
より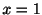 は不確定特異点.他の2つの特異点は確定特異点.
は不確定特異点.他の2つの特異点は確定特異点.
通常点のときと同様,確定特異点のまわりにも級数解が存在します.
この級数
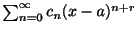 はFrobenius級数(Frobinius series)とよばれ,この級数を解として
はFrobenius級数(Frobinius series)とよばれ,この級数を解として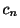 を求める方法をFrobenius法といいます.次の例題でFrobenius法の用い方を説明します.
を求める方法をFrobenius法といいます.次の例題でFrobenius法の用い方を説明します.
例題 4.4
次の微分方程式の
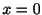
のまわりでの級数解を求めよ.
解
より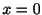 は確定特異点.よって解を
は確定特異点.よって解を
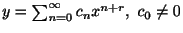 とおく.これを微分することにより得られる
を元の式に代入すると
となる.ここで
とおく.これを微分することにより得られる
を元の式に代入すると
となる.ここで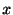 のベキを必ず一番小さいものにそろえると
次に級数のインデックスを一番大きなものにそろえると
となる.ここで
のベキを必ず一番小さいものにそろえると
次に級数のインデックスを一番大きなものにそろえると
となる.ここで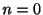 のときでてきた方程式
のときでてきた方程式
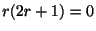 を決定方程式(indicial equation)という.この方程式を解くと
を決定方程式(indicial equation)という.この方程式を解くと
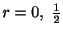 .
これより2つの一次独立な級数解
を得る.また
.
これより2つの一次独立な級数解
を得る.また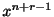 の係数を0とおくと漸化式
を得る.ここで
の係数を0とおくと漸化式
を得る.ここで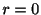 とおくと
とおくと
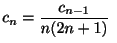
より
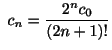
となるので,
また
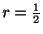 とおくと
とおくと
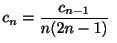
より
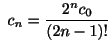
となるので,
例題 4.5
次の微分方程式の
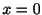
のまわりでの級数解をひとつ求めよ.
解
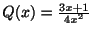 より
より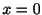 は確定特異点.そこで
は確定特異点.そこで
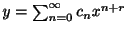 とおくと,
とおくと,
となる.ここでベキを一番小さな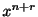 でそろえると,
次に級数のインデックスを一番大きなものでそろえると
を得る.
決定方程式は
でそろえると,
次に級数のインデックスを一番大きなものでそろえると
を得る.
決定方程式は
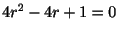 となるので,
となるので,
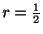 .また漸化式
.また漸化式
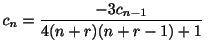
より
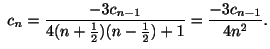
よって,ひとつの解は
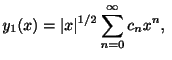
ただし
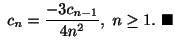
上の例題の解答は完全でありません.一次独立な解が2つあるはずです.ではもうひとつの解はどうやったら求まるのでしょうか.すでに学びましたが,ひとつの解がわかっているときは,階数低減法を用いてもうひとつの解を求めることができます.ここでは証明しませんが,もうひとつの解は次のように表わされることがわかっています.
例題 4.6
次の微分方程式の
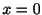
のまわりでの級数解を求めよ.
解
上の例題で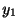 はすでに求めたので,
はすでに求めたので,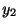 を求める.定理より,
を求める.定理より,
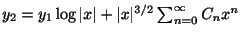 の形をした解を探す.計算の都合上
の形をした解を探す.計算の都合上
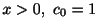 とおく.
とおく.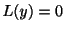 に
に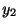 を代入すると
を代入すると
となる.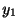 の最初の何項かを表わすと
ここで
の最初の何項かを表わすと
ここで
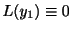 を用いると
これより
を用いると
これより
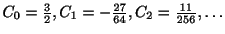 . よって
. よって
例題 4.7
次の微分方程式の
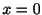
のまわりでの級数解を求めよ.
解
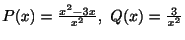 より
より は確定特異点.そこで
は確定特異点.そこで
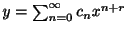 とおくと
とおくと
ここでベキを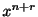 でそろえると
これより
でそろえると
これより
を得る.ここで決定方程式
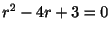 より
より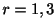 .よって2つの解
を得る.また
.よって2つの解
を得る.また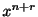 の係数を0とおくことより,漸化式
を得る.
の係数を0とおくことより,漸化式
を得る.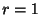 のとき
のとき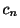 を求めると
となる.また
を求めると
となる.また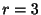 のとき
のとき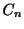 を求めると
ところが
を求めると
ところが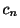 と
と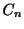 はよく見ると
はよく見ると
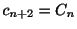 .つまり
.つまり
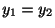 .
そこでもうひとつ一次独立な解を探さなければならない.そのために次のような定理がある.
.
そこでもうひとつ一次独立な解を探さなければならない.そのために次のような定理がある.
これより上の例題のもうひとつの解は
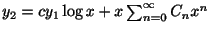 を
を
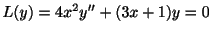 に代入することにより求めることができる.
に代入することにより求めることができる.
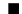





: 演習問題
: 級数による解法
: 演習問題
目次
索引
Administrator
平成26年9月18日
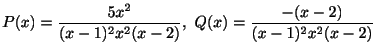
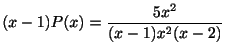
![]() はFrobenius級数(Frobinius series)とよばれ,この級数を解として
はFrobenius級数(Frobinius series)とよばれ,この級数を解として![]() を求める方法をFrobenius法といいます.次の例題でFrobenius法の用い方を説明します.
を求める方法をFrobenius法といいます.次の例題でFrobenius法の用い方を説明します.
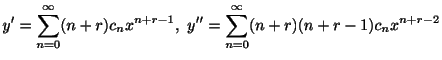
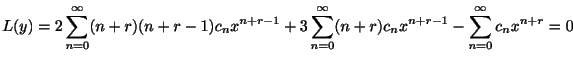
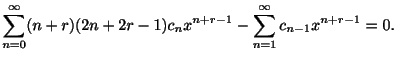
![$\displaystyle \underbrace{r(2r-1)c_{0}x^{r-1}}_{n = 0} + \sum_{n=1}^{\infty}[(n+r)(2n+2r+1)c_{n} - c_{n-1}]x^{n+r-1} = 0 $](img1248.gif)
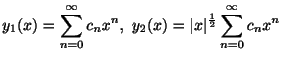
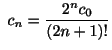
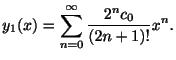
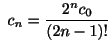
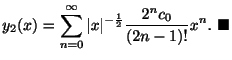
![]() より
より![]() は確定特異点.そこで
は確定特異点.そこで
![]() とおくと,
とおくと,
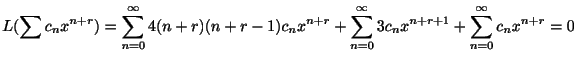
![$\displaystyle \sum_{n=0}^{\infty}[4(n+r)(n+r-1) + 1]c_{n}x^{n+r} + \sum_{n=1}^{\infty}3c_{n-1}x^{n+r} = 0. $](img1268.gif)
![$\displaystyle \underbrace{(4r(r-1) + 1)c_{0}x^{r}}_{n = 0} + \sum_{n=1}^{\infty}\{[4(n+r)(n+r-1) + 1]c_{n} + 3c_{n-1}\}x^{n+r} = 0 $](img1269.gif)
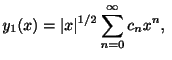 ただし
ただし![]() はすでに求めたので,
はすでに求めたので,![]() を求める.定理より,
を求める.定理より,
![]() の形をした解を探す.計算の都合上
の形をした解を探す.計算の都合上
![]() とおく.
とおく.![]() に
に![]() を代入すると
を代入すると
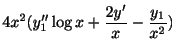
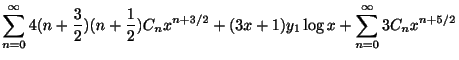
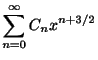
![$\displaystyle \sum_{n=1}^{\infty}[4(n + \frac{3}{2})(n + \frac{1}{2})C_{n} + C_{n} + 3C_{n-1}]x^{n+3/2} = 0$](img1287.gif)
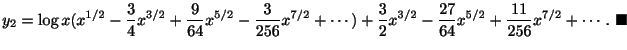
![]() より
より![]() は確定特異点.そこで
は確定特異点.そこで
![]() とおくと
とおくと
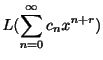
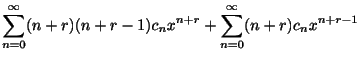
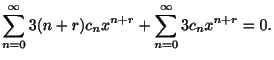
![$\displaystyle \sum_{n=0}^{\infty}[(n+r)(n+r-1) - 3(n+r) + 3]c_{n}x^{n+r} + \sum_{n=1}^{\infty}(n+r-1)c_{n-1}x^{n+r} = 0. $](img1299.gif)
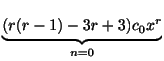
![$\displaystyle \sum_{n=1}^{\infty}\{[(n+r)(n+r-1) - 3(n+r) + 3]c_{n} + (n+r-1)c_{n-1}\}x^{n+r} = 0$](img1301.gif)
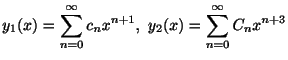
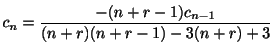
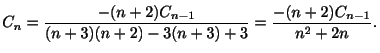
![]() を
を
![]() に代入することにより求めることができる.
に代入することにより求めることができる.
![]()