next up previous contents index
: 演習問題 : 1階微分方程式 : 1階微分方程式   目次   索引

微分方程式

物理学，化学，そして工学における自然の法則の多くが微分方程式を用いて表わすことができます．それらの法則の中からこの本の中でとりあげるものだけでも Newton の第 2 法則，Newton の冷却の法則，Kirchhoff の第2法則，熱伝導の Fourier の法則，波動方程式，振動方程式，化学反応方程式などがあります．このように，現象を数学的に定式化すると，微分方程式の形になって表われるものが少なくありません．

微分方程式とは未知関数とその導関数からなる関係式のことをいいます．これから考える微分方程式の多くは，積分を有限回行なってこの未知関数を求める求積法 (quadrature) とよばれる方法で解けますが，多くの微分方程式は求積法では解が得られません．そこで求積法で解けない微分方程式では解を級数，数値計算，グラフを使って近似します．

独立変数$ x$とその関数$ y(x)$および導関数 $ y^{\prime},y^{\prime \prime},\ldots,y^{(n)}$の間の関係式

$\displaystyle F(x,y(x),y^{\prime}(x),\ldots,y^{(n)}(x)) = 0 $

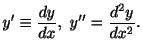を$ y$に関する常微分方程式 (ordinary differential equation) といいます．常微分方程式の例をいくつかあげてみます．( $ \displaystyle{y^{\prime} \equiv \frac{dy}{dx}, \ y^{\prime\prime} = \frac{d^{2}y}{dx^{2}}. }$)

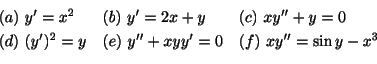
\begin{displaymath}\begin{array}{lll} (a) \ y^{\prime} = x^{2} &(b) \ y^{\prime}... ...e} = 0 & (f) \ xy^{\prime\prime} = \sin{y} - x^{3} \end{array}\end{displaymath}

微分方程式に含まれる導関数の最高階数を，その微分方程式の階数 (order) といいます．方程式 $ (a),(b),(d)$は1階で残りは2階の微分方程式となります．先に述べた自然の法則の多くは，1階か2階の微分方程式で定式化できるので，この本ではこの2つの階数の微分方程式を主にとりあげます．

微分方程式が次の形で表わせるとき，つまり未知関数とその導関数についての一次式で表わせるとき，線形 (linear) であるといい，そうでないときを非線形 (nonlinear) であるといいます．よって，$ n$ 階の線形微分方程式は次の形で表わせます．

$\displaystyle a_{n}y^{(n)} + a_{n-1}y^{(n-1)} + \cdots + a_{1}y^{\prime} + a_{0}y = b(x), $

ただし $ y^{(n)} \equiv \frac{d^{n}}{dx^{n}y}$．また この定義より方程式 $ (a)-(c)$ は線形，$ (d)-(f)$ は非線形といえます．線形微分方程式には線形代数を基本にしたエレガントな理論があります．ただ1階の微分方程式に関していえば，線形であるということはそれほど重要ではありません．そこで第1章では線形，非線形を問わず1階の微分方程式の解法としてこれまでに開発されてきた求積法について学びます．

微分方程式に代入したとき，方程式をある区間上で恒等的に満たすような関数を微分方程式の解 (solution) といい，解を求めることを微分方程式を解く (solve) といいます．解はいつも $ y = f(x)$ という式で与えられるわけではありません．ときには陰関数 $ G(x,y) = 0$ の形で与えられることもあります．

例題 1.1   $ e^{x},e^{x+c},ce^{x}$は $ y^{\prime} = y$の解であることを示せ．また $ e^{2x},e^{x}+c \ (c \neq 0)$は $ y^{\prime} = y$の解ではないことを示せ．

解 $ e^{x},e^{x+c},ce^{x}$の導関数はそれ自身であるから $ y^{\prime} = y$の解である． また $ (e^{2x})^{\prime} = 2e^{2x} \not\equiv e^{2x}, (e^{x}+c)^{\prime} = e^{x} \not\equiv e^{x}+c \ (c \neq 0)$より， $ y^{\prime} = y$の解でない． $ \ \blacksquare$

例題 1.2   $ y_{1} = x^{5} + x^{4}$と $ y_{2} = x^{5}$は $ y^{\prime} = 4(y/x) + x^{4}$の解であることを示せ．

解 $ y_{1}^{\prime} = 5x^{4} + 4x^{3}$と $ 4(y_{1}/x) + x^{4} = (4x^{5} + 4x^{4})/x + x^{4} = 5x^{4} + 4x^{3}$より，$ y_{1}(x)$は解である．また $ y_{2}^{\prime} = 5x^{4}$と $ 4(y_{2}/x) + x^{4} = 4x^{5}/x + x^{4} = 5x^{4}$より，$ y_{2}(x)$も解である． $ \ \blacksquare$

これらの例からもわかるように，微分方程式の解はひとつとは限りません．一般に$ n$階の微分方程式では，任意にその値をとることができる$ n$個の定数を含む解が存在します．この解をその方程式の一般解(general solution)といいます．また一般解の任意定数にある特定の値を入れてできた解を特殊解(particular solution)といいます．たとえば $ y^{\prime} = y$の一般解は $ y = ce^{x}$で与えられ， $ x = 0,y = 1$を代入して得られた$ y = e^{x}$は特殊解です．

2つの変数$ x, y$からなる微分方程式の一般解は上の例でもわかるように$ xy$平面で曲線群を描きます．そのとき表われる各曲線を解曲線(solution curve)または積分曲線(integral curve)といいます．

微分方程式 $ F(x,y,y^{\prime},\cdots,y^{(n)}) = 0$について，$ x$のある値$ x_{0}$における$ y$の$ n-1$階までの導関数の値をあらかじめ指定する条件

$\displaystyle y(x_{0}) = y_{0}, y^{\prime}(x_{0}) = y_{1},\ldots,y^{(n-1)}(x_{0}) = y_{n-1} $

を初期条件(initial condition)といいます．またこの条件を満たす解を求める問題を初期値問題(initial value problem)といいます．いい換えると初期条件を満たす解曲線を求める問題のことです．

微分方程式 $ F(x,y,y^{\prime},\cdots,y^{(n)}) = 0$を区間$ [a,b]$で考えたとき，区間の両端 $ x = a, x = b$において，解または解の導関数が満たすべき条件を境界条件(boundary condition)といいます．またこの条件を満たす解を求める問題を，境界値問題(boundary value problem)といいます．いい換えると境界条件を満たす解曲線を求める問題のことです．

これから私たちは常微分方程式の初期値問題について学んでいきます．



Administrator 平成26年9月18日