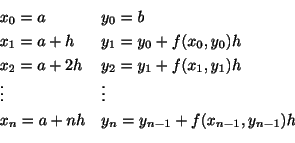next up previous contents index
: 演習問題 : 1階微分方程式 : 演習問題   目次   索引

数値計算法

ここでは1階の微分方程式 $ y^{\prime} = f(x,y)$について考えます．この微分方程式は平面上の点$ (x,y)$における関数$ y$の傾きを表わしていると考えることができます．よって各点 $ (x_{0},y_{0})$に傾き $ f(x_{0},y_{0})$を合わせたものを考えます．これをグラフであらわすためにまず $ f(x,y) = c$を満たす曲線を描きます．この曲線は等傾曲線(isocline)とよばれています．そしてこの曲線上にいくつもの点をとり，それぞれの点で傾き$ f(x,y)$をもった短い線分を描きます．この線分の集まりを微分方程式 $ y^{\prime} = f(x,y)$の方向場(direction field)といいます．とくに初期値問題の解曲線は初期値 $ (x_{0},y_{0})$から方向場に沿って描かれた曲線で表わすことができます．

私たちはここまで微分方程式の解を形式的に求めてきました．そのため特異解については考えないことにしてきました．ここでは方向場を用いて特異解を含めた完全解(complete solution)について学びます．

例題 1.27   $ y^{\prime} = \sqrt{1 - y^{2}}$の完全解を求めよ．

解 形式的に解くと変数分離形より

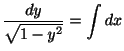
$\displaystyle \frac{dy}{\sqrt{1-y^{2}}} = \int dx $

$\displaystyle \sin^{-1}{y} = x + c $

$\displaystyle y = \sin{(x + c)} $

となる．ところがこの解はどこか変である．元の微分方程式をみると $ y^{\prime}$は負にならない．しかし求めた解の導関数は負になる．そこで等傾曲線を用いて方向場を描く．

図 1.2: 解曲線
\begin{figure}\begin{center} \includegraphics[width=10cm]{DFQ/Fig1-2.eps} \end{center}\end{figure}

これから $ y \equiv 1, \ y \equiv -1$も解であることがわかる．また正弦曲線が$ y = 1$と$ y = -1$に滑らかにつながっている．これより完全解は $ y = 1$または$ y = -1$または

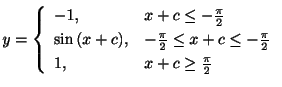
$\displaystyle y = \left\{\begin{array}{ll} -1, & x+c \leq -\frac{\pi}{2} \\ \s... ...\leq x+c \leq -\frac{\pi}{2}\\ 1, & x+c \geq \frac{\pi}{2} \end{array}\right. $

となる． $ \ \blacksquare$

次にグラフによる解法から数値解を得ることを考えます．グラフによる解法では方向場を用いて解曲線を得ます．残念ながら他の情報が与えられない限り直接グラフから解曲線の方程式を求めることはできません．しかし解曲線の傾きの変化を短い区間ごとに描くと，近似曲線は多角直線になり，それぞれの区間における直線の式を求めることができます．

点 $ (x_{0},y_{0})$を通る近似直線の傾きは $ f(x_{0},y_{0})$より，その方程式は

$\displaystyle y = f(x_{0},y_{0})(x - x_{0}) + y_{0} . $

これより $ x_{1} = x_{0} + h$のとき， $ y_{1} = f(x_{0},y_{0})h + y_{0}$を得ます．次に点 $ (x_{1},y_{1})$と傾き $ f(x_{1},y_{1})$より

$\displaystyle y = f(x_{1},y_{1})(x - x_{1}) + y_{1} . $

これを目的の$ x$の値にとどくまで繰り返します．

例題 1.28   $ y^{\prime} = y + x^{2}, y(0) = 1$のとき$ y(3)$の値を求めよ．ただし$ h = 1$とする．

解 $ (x_{0},y_{0}) = (0,1)$より$ y = 1 + x$を得る．つぎに $ (x_{1},y_{1}) = (1,2)$より $ y = 3x - 1$．最後に $ (x_{2},y_{2}) = (2,5)$より $ y = 9x - 13$．よって$ y(3) = 14$となる．この問題は線形なので求積法で求めることができ $ y = 3e^{x} - x^{2} - 2x - 2$となる，よって $ y(3) = 3e^{3} - 17 \doteq 43.3$となる． $ \ \blacksquare$

気づいたと思いますがこの場合，近似直線による方法には誤差がかなりあります．誤差を少なくするためには$ h$をもっと小さくすればよいのですが$ h$を小さくすると計算が面倒になります．そこでコンピュータを使って計算します．あまり実用的ではありませんが，もっと実用的なものの基礎となっているEuler法(Euler's method)とよばれている簡単なアルゴリズムを記しておきます．
初期値問題

$\displaystyle y^{\prime} = f(x,y), \ y(a) = b$

の近似解は次の方法で求まる．

\begin{displaymath}\begin{array}{ll} x_{0} = a & y_{0} = b\\ x_{1} = a + h & y_... ...} = a + nh & y_{n} = y_{n-1} + f(x_{n-1},y_{n-1})h \end{array} \end{displaymath}



Administrator 平成26年9月18日