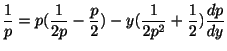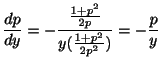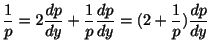: 演習問題
: 1階微分方程式
: 演習問題
目次
索引
1階微分方程式
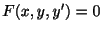 が
が
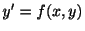 で書き表されるとき,この微分方程式を正規形方程式とよびます.これまで学んできた微分方程式はすべて正規形でした.ここでは,正規形ではない微分方程式について学びます.
簡略化のために,以下では記号
を用います.
で書き表されるとき,この微分方程式を正規形方程式とよびます.これまで学んできた微分方程式はすべて正規形でした.ここでは,正規形ではない微分方程式について学びます.
簡略化のために,以下では記号
を用います.
例題 1.22
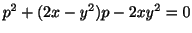
を解け.
解 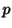 について求める.因数分解すると
について求める.因数分解すると
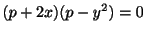 となる.この式を満たすには
となる.この式を満たすには
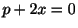 または
または
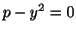 を満たすことである.
を満たすことである.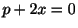 の一般解は
の一般解は
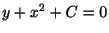 . また,
. また,
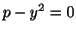 は変数分離より一般解は
は変数分離より一般解は
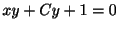 となる.これより,求める一般解は
となる.
となる.これより,求める一般解は
となる.
例題 1.23
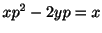
を解け.
解 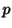 について求めると,解の公式より,
ここで,
について求めると,解の公式より,
ここで,
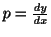 より,この式は同次形となる.したがって
より,この式は同次形となる.したがって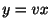 とおくと,
とおくと,
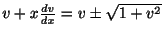 . これより,
よって,
こうして一般解は
これを変形すると,
. これより,
よって,
こうして一般解は
これを変形すると,
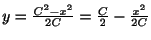
例題 1.24
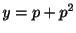
を解け.
解 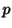 について解くと,
となり,これまで学んだどのテクニックでも解けない.そこで,別の方法を考える.
について解くと,
となり,これまで学んだどのテクニックでも解けない.そこで,別の方法を考える.
まず,両辺を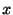 で微分すると,
で微分すると,
したがって,
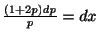 より,
より,
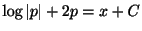 . よって,一般解は
. よって,一般解は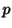 をパラメターとする表示
と表す.
をパラメターとする表示
と表す.
例題 1.25
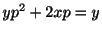
を解け.
解 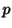 について解くと,
について解くと,
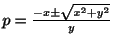 . これは同次形であるが,
. これは同次形であるが,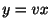 とおいたのでは解けない.そこで,別の方法を考える.
この式は
とおいたのでは解けない.そこで,別の方法を考える.
この式は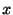 について解くことができ,
について解くことができ,
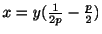 となる.この両辺を
となる.この両辺を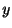 で微分すると,
これより,
整理すると,
で微分すると,
これより,
整理すると,
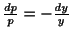 より
より
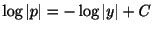 ,
, 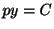 となる.これを用いて
となる.これを用いて
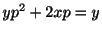 から
から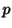 を消去すると,一般解
を得る.
を消去すると,一般解
を得る.
例題 1.26
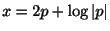
を解け.
解 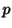 について解くことができないので,両辺を
について解くことができないので,両辺を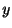 で微分すると,
これより,
で微分すると,
これより,
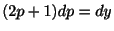 ,
,
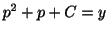 となり,一般解は
となり,一般解は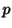 をパラメターとして,
をパラメターとして,
Administrator
平成26年9月18日
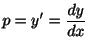
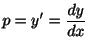
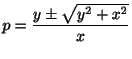
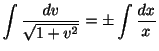
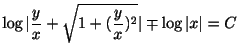
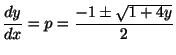
![]() で微分すると,
で微分すると,
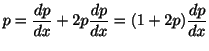
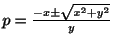 . これは同次形であるが,
. これは同次形であるが,