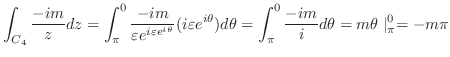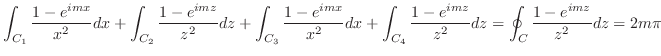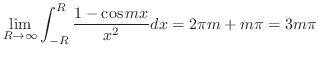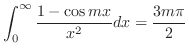Next: 索引 Up: 演習問題詳解 Previous: 5.2 留数 索引
1.
![\includegraphics[width=6cm]{COMPFIG/Fig-counter.eps}](img925.png)
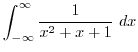
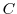 を実軸上の
を実軸上の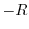 と
と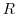 を結ぶ直線と
を結ぶ直線と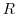 と
と を結ぶ半径
を結ぶ半径 ,中心0の曲線
,中心0の曲線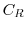 とすると,
とすると,
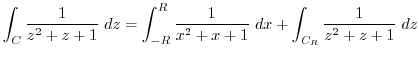
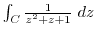 を求めると,特異点は
を求めると,特異点は
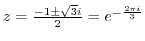 であるが,
であるが,
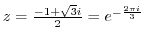 だけが曲線
だけが曲線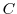 の内部にあるので,留数定理により
の内部にあるので,留数定理により
![$\displaystyle \int_{C}\frac{1}{(z^2 +1)(z^2 +4)} dz = 2\pi i(Res[e^{-\frac{2\pi i}{3}}])$](img933.png)
![$\displaystyle Res[\frac{-1 + \sqrt{3}i}{2}]$](img934.png) |
 |
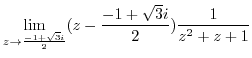 |
|
 |
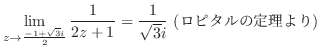 |
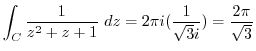
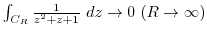 を示せれば,
を示せれば,
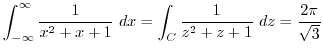
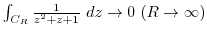 を示す.
を示す.
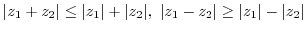
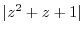 |
 |
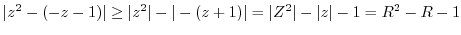 |
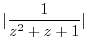 |
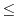 |
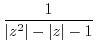 |
|
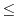 |
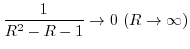 |
![\includegraphics[width=6cm]{COMPFIG/Fig-counter.eps}](img925.png)
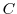 を実軸上の
を実軸上の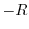 と
と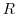 を結ぶ直線と
を結ぶ直線と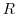 と
と を結ぶ半径
を結ぶ半径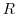 ,中心0の曲線
,中心0の曲線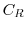 とすると,
とすると,
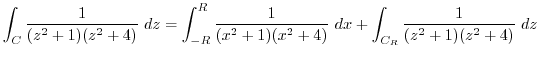
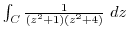 を求めると,特異点は
を求めると,特異点は
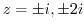 であるが,
であるが,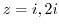 だけが曲線
だけが曲線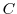 の内部にあるので,留数定理により
の内部にあるので,留数定理により
![$\displaystyle \int_{C}\frac{1}{(z^2 +1)(z^2 +4)} dz = 2\pi i(Res[i] + Res[2i])$](img952.png)
![$\displaystyle Res[i] = \lim_{z \to i}(z - i)\frac{1}{(z^2 + 1)(z^2 + 4)} = \lim_{z \to i}\frac{1}{(z+i)(z^2 +4)} = \frac{1}{2i(3)} = \frac{1}{6i}$](img953.png)
![$\displaystyle Res[2i] = \lim_{z \to 2i}(z - 2i)\frac{1}{(z^2 + 1)(z^2 + 4)} = \lim_{z \to 2i}\frac{1}{(z^2 + 1)(z + 2i)} = \frac{1}{-3(4i)} = \frac{-1}{12i}$](img954.png)
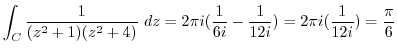
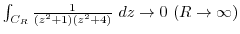 を示せれば,
を示せれば,
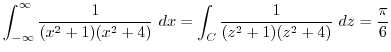
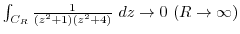 を示す.
を示す.
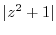 |
 |
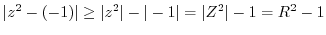 |
|
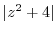 |
 |
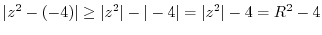 |
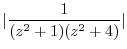 |
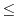 |
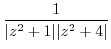 |
|
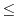 |
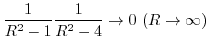 |
三角関数の積分である.ここで,曲線 は中心が原点で半径1の円であるので,
は中心が原点で半径1の円であるので,
 とおく.次に,
とおく.次に,
 を
を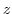 を用いて表すと,.
を用いて表すと,.
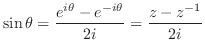
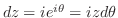 . よって,
. よって,
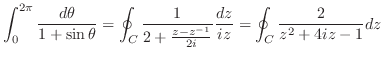
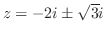 であるが,
であるが,
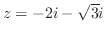 は曲線
は曲線 の外側である. したがって,
の外側である. したがって,
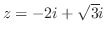 の留数を求めればよい.
の留数を求めればよい.
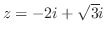 は第1位の曲であるので,
は第1位の曲であるので,
![$\displaystyle Res[-2i + \sqrt{3}i] = \lim_{z \to -2i + \sqrt{3}i}(z - (-2i + \s...
...^2 + 4iz -1}= \lim_{z \to -2i + \sqrt{3}i}\frac{2}{2z+4i} = \frac{1}{\sqrt{3}i}$](img972.png)
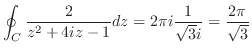
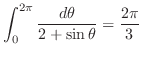
(d)
この積分を求めるには, 曲線  を
を
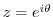 で表す. すると
で表す. すると
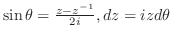 となる.よって,
となる.よって,
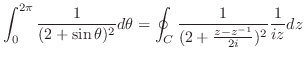
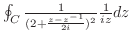 .
.
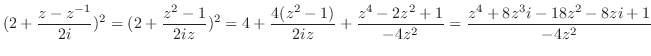
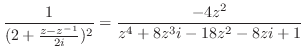
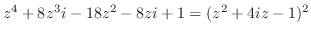 と表せるので,特異点は
と表せるので,特異点は
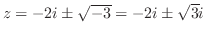 . ただし,
. ただし,
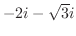 は曲線
は曲線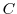 の外側であるから,
の外側であるから,
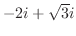 の留数だけを求めればよい.
の留数だけを求めればよい.
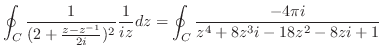
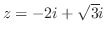 は第2位の極である. よって,
は第2位の極である. よって,
![$\displaystyle Res[-2i + \sqrt{3}i] = \lim_{z \to -(2-\sqrt{3})i}\left(\frac{4\p...
...{(z -(-2-\sqrt{3}i)^2}\right)' = \frac{32\sqrt{3}i}{48} = \frac{-2\sqrt{3}i}{3}$](img985.png)
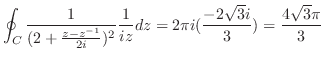
![\includegraphics[width=6cm]{COMPFIG/Fig-counter.eps}](img925.png)
点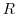 と
と 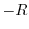 を結ぶ曲線
を結ぶ曲線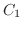 , 点
, 点 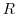 と点
と点 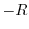 を結ぶ曲線
を結ぶ曲線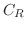 とする. 曲線
とする. 曲線 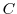 はこの直線
はこの直線 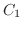 と曲線
と曲線 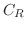 でできているとする.ここでは,次のような積分を考える.
でできているとする.ここでは,次のような積分を考える.
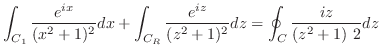
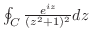 の値を求める.
の値を求める.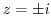 が特異点であるが,
が特異点であるが,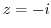 は曲線
は曲線 の外部である.
そこで,
の外部である.
そこで,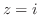 の留数を求めると
の留数を求めると 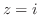 は第2位の極であるので,
は第2位の極であるので,
![$\displaystyle Res[i] = \lim_{z \to i}\left((z-i)^2\frac{e^{iz}}{(z+i)^2 (z-i)^2}\right)' = \frac{-ie^{-1}}{2}$](img992.png)
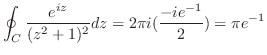
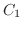 上での積分を行う.
上での積分を行う.
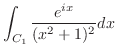 |
 |
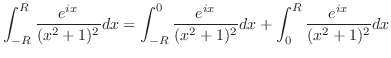 |
|
 |
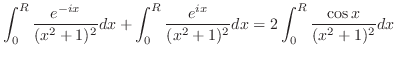 |
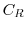 上での積分を行う.
上での積分を行う.
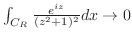 が
が
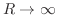 で収束することを示す.
で収束することを示す.
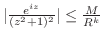 となる
となる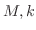 が存在することを示せばよい.
が存在することを示せばよい.
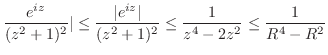
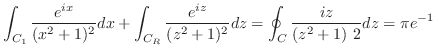
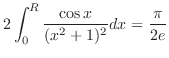
![\includegraphics[width=6cm]{COMPFIG/Fig-counter.eps}](img925.png)
点 と
と 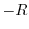 を結ぶ曲線
を結ぶ曲線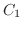 , 点
, 点 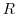 と点
と点 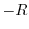 を結ぶ曲線
を結ぶ曲線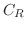 とする. 曲線
とする. 曲線 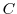 はこの直線
はこの直線 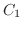 と曲線
と曲線 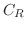 でできているとする.ここでは,次のような積分を考える.
でできているとする.ここでは,次のような積分を考える.
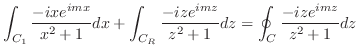
まず,留数定理を用いて
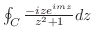 の値を求める.
の値を求める. 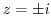 が特異点であるが,
が特異点であるが, 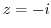 は曲線
は曲線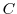 の外部である. そこで,
の外部である. そこで, 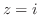 の留数を求めると
の留数を求めると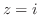 は1位の極なので.
は1位の極なので.
![$\displaystyle Res[i] = \lim_{z \to i}\frac{-ize^{imz}}{(z+i)(z-i)} = \frac{e^{-m}}{2i}$](img1006.png)
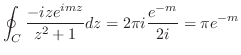
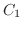 上での積分を考える.
上での積分を考える.
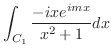 |
 |
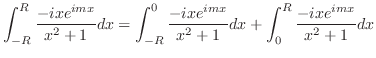 |
|
 |
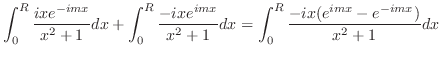 |
||
 |
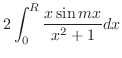 |
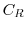 上での積分を行う.
上での積分を行う.
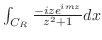 が
が
 で0に収束することを示す.
で0に収束することを示す. 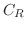 において
において
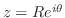 であるから
であるから
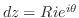 そして,
そして,
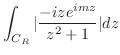 |
 |
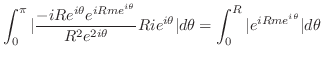 |
|
 |
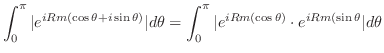 |
||
 |
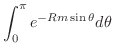 |
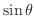 のグラフを考える.
のグラフを考える.
![$[0, \frac{\pi}{2}]$](img1019.png) と
と
![$[\frac{\pi}{2},\pi]$](img1020.png) とに積分を分けると,
とに積分を分けると,
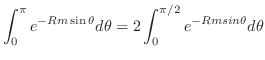
![$[0, \frac{\pi}{2}]$](img1019.png) において,
において,
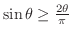 が成り立つ. したがって,
が成り立つ. したがって,
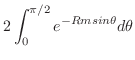 |
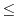 |
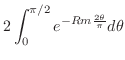 |
|
 |
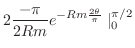 |
||
 |
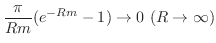 |
これより,
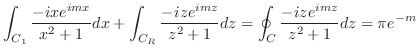
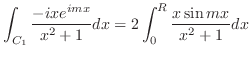
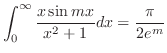
![\includegraphics[width=7cm]{COMPFIG/Fig-counter2.eps}](img1030.png)
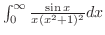 を解くには, 点0が特異点であることに注意し,点
を解くには, 点0が特異点であることに注意し,点
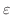 と点
と点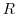 を結ぶ直線を
を結ぶ直線を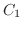 , 点
, 点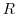 と
と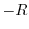 を結ぶ曲線
を結ぶ曲線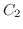 , 点
, 点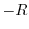 と点
と点
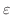 を結ぶ直線
を結ぶ直線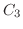 , 点
, 点
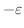 と点
と点
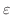 を結ぶ曲線
を結ぶ曲線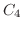 を考える. 曲線
を考える. 曲線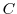 は
は
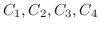 でできている.
ここでは,次のような積分を考える.
でできている.
ここでは,次のような積分を考える.
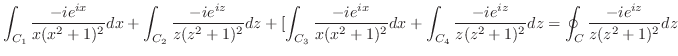
まず,留数定理を用いて
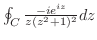 の値を求める.
の値を求める.
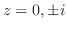 は得点であるが
は得点であるが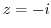 は曲線
は曲線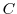 の外部である. そこで
の外部である. そこで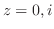 の留数を求める.
の留数を求める.
![$\displaystyle Res[0] = \lim_{z \to 0}\frac{-zie^{iz}}{z(z^2 + 1)^2} = -i$](img1042.png)
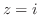 の留数を求める.
の留数を求める.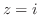 は2位の極であるので,
は2位の極であるので,
![$\displaystyle Res[i] = \lim_{z \to i}\left((z-i)^2\frac{-ie^{iz}}{z(z^2 + 1)^2}\right)' = \frac{-12ie^{-1}}{-16} = \frac{3i}{4e}$](img1043.png)
 と
と における積分を行う.
における積分を行う.
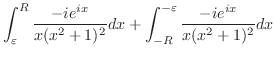
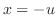 とおくと,
とおくと,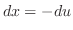 ,
,
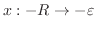 ,
,
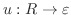 . これより,
. これより,
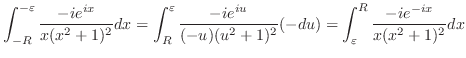
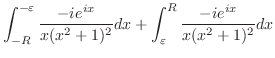 |
 |
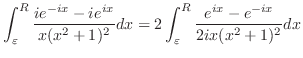 |
|
 |
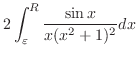 |
 における積分を行う.
における積分を行う.
 が
が
 で0に収束することを示す.
で0に収束することを示す.
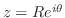 より,
より,
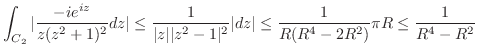
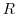 goes to
goes to 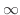 で0に収束する.この結果,
で0に収束する.この結果,
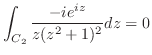
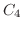 における積分を行う.
における積分を行う.
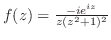 を
を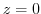 の周りでのLaurent展開をすでに行っている.それによると,
の周りでのLaurent展開をすでに行っている.それによると,
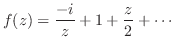
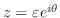 より
より
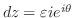 . よって,
. よって,
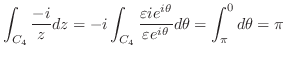
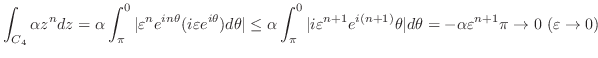
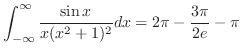
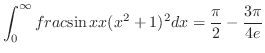
![\includegraphics[width=7cm]{COMPFIG/Fig-counter2.eps}](img1030.png)
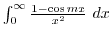 を解くには,点
を解くには,点
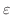 と点
と点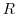 を結ぶ直線を
を結ぶ直線を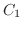 , 点
, 点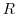 と
と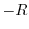 を結ぶ曲線
を結ぶ曲線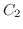 , 点
, 点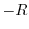 と点
と点
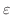 を結ぶ直線
を結ぶ直線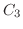 , 点
, 点
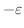 と点
と点
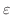 を結ぶ曲線
を結ぶ曲線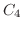 を考える. 曲線
を考える. 曲線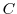 は
は
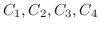 でできている.
ここでは,次のような積分を考える.
でできている.
ここでは,次のような積分を考える.
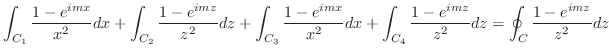
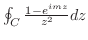 の値を求める.
の値を求める.
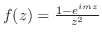 を
を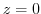 のまわりでLaurent展開する.
のまわりでLaurent展開する.
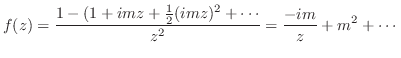
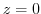 は1位の極でその留数は
は1位の極でその留数は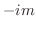 である. したがって,
である. したがって,
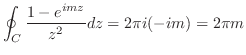
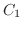 と
と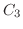 上で積分を行う.
上で積分を行う.
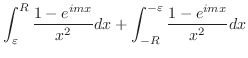
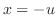 とおくと
とおくと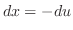 ,
,
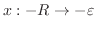 ,
,
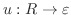 より,
より,
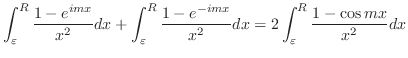
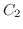 上において積分を行う.
上において積分を行う.
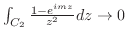 が
が
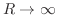 で0に収束することを示す.
で0に収束することを示す.
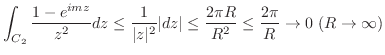
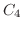 上において積分を行う.
上において積分を行う.
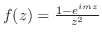 とし,
とし,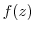 を
を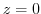 の周りでLaurent展開すると,
の周りでLaurent展開すると,
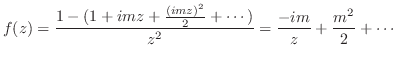
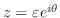 とおくと
とおくと
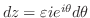 . また,
. また, 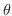 は
は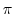 から0に移る. まず,第1項について積分すると
から0に移る. まず,第1項について積分すると