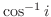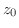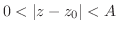Next: 正則関数 Up: 複素関数 Previous: 初等関数(elementary functions) 索引
 と
と の間に
の間に
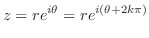
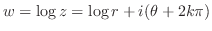
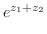 を持っているので,
を持っているので,
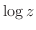
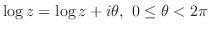
 は,1つの複素数
は,1つの複素数 に対して無限個の異なる値が対応する.すなわち無限多価関数である.
に対して無限個の異なる値が対応する.すなわち無限多価関数である. の 主値(principal value)または 主分岐(main branch)は
の 主値(principal value)または 主分岐(main branch)は
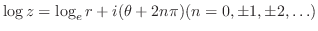
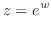 の区間なら他の区間でもよい.例えば
の区間なら他の区間でもよい.例えば
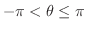 .
.
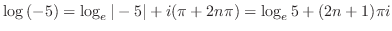 の値を求めよ.
の値を求めよ.
解
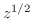 を用いる.
を用いる.
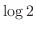
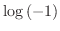 は2つの分岐を持つことを示せ.
は2つの分岐を持つことを示せ.
2. 次の値を全て求めよ.
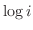
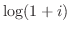
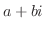
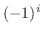
3. 次の値を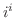 の形で表せ.
の形で表せ.
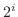
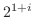
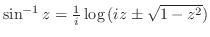
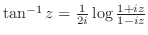
4. 次の公式を証明せよ.
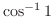
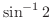
(5) 次の値を求めよ.