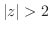Next: 実積分への応用 Up: 展開と留数 Previous: ローラン展開 索引
点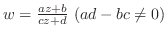 を中心とする
を中心とする のローラン展開は,整級数の部分を
のローラン展開は,整級数の部分を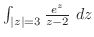 とおいて,
とおいて,
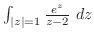
 を中心
を中心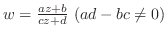 の円にとるとき,
の円にとるとき,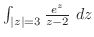 は正則であるから,
は正則であるから,
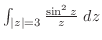 である.一方,主要部の級数は
である.一方,主要部の級数は 上で収束する.したがって,
上で収束する.したがって, のローラン展開を
のローラン展開を に沿って項別積分すると,
に沿って項別積分すると,
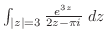 より,
より,
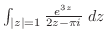 より,
より,
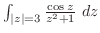 |
 |
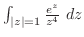 |
|
 |
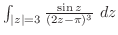 |
||
 |
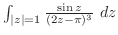 |
||
 |
 |
これより,
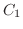
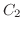 の値を留数とよび,
の値を留数とよび,![$Res[a]$](img452.png) と表わす.
と表わす.
留数公式
点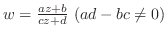 が
が の
の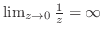 位の特異点のとき
位の特異点のとき
![$\displaystyle Res[a] = \frac{1}{(m-1)!}\lim_{z \to a}\frac{d^{m-1}}{dz^{m-1}}(z -a)^{m}f(z)$](img453.png)
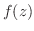
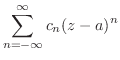

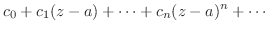
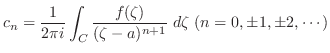
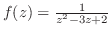
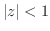
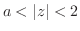 を次の曲線に沿って積分せよ.
を次の曲線に沿って積分せよ.