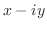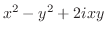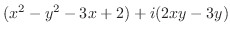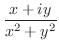Next: 複素積分 Up: 正則関数(analytic function,holomorphic function) Previous: 微分係数と導関数 索引
領域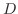 で定義された関数
で定義された関数
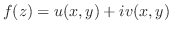 が
が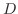 内の点
内の点
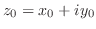 で微分可能だとする.このとき,
で微分可能だとする.このとき,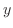 を一定に保ちながら
を一定に保ちながら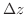 を0に近づけると
を0に近づけると
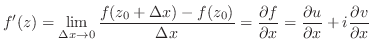
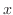 を一定に保ちながら
を一定に保ちながら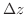 を0に近づけると
を0に近づけると
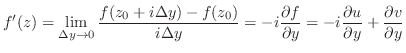
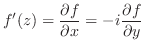
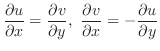
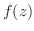 がその定義域
がその定義域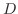 のすべての点で微分可能なとき,
のすべての点で微分可能なとき,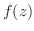 は
は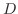 で正則(analytic)であるという.
で正則(analytic)であるという.
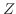 平面全体
平面全体
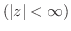 で正則な関数を整関数という.
で正則な関数を整関数という.
注1. 点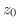 で正則というときは,
で正則というときは,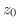 だけでなくその近傍を含めて正則なことを意味する.
だけでなくその近傍を含めて正則なことを意味する.
注2. 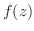 が正則ならば,(微分可能であるから)連続である.
が正則ならば,(微分可能であるから)連続である.
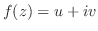 が
が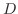 で正則のとき,
で正則のとき,
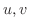 の第2次偏導関数も連続とすれば,
の第2次偏導関数も連続とすれば,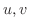 は調和関数(harmonic function)である.すなわち Laplaceの微分方程式を満たす.
は調和関数(harmonic function)である.すなわち Laplaceの微分方程式を満たす.
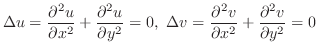
注  が連続な第2次偏導関数をもつことを仮定したが,正則関数は何回でも微分可能なことが別に証明されているから,この仮定はいらない.
が連続な第2次偏導関数をもつことを仮定したが,正則関数は何回でも微分可能なことが別に証明されているから,この仮定はいらない.
注 定理3.4の十分条件を強くしたもので,正則性の判定に有効である.
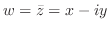 では,
では,
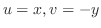 で
で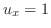 と
と
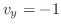 とが等しくないから,Cauchy-Riemannの方程式(正則の必要条件)が成り立たない.よって,
とが等しくないから,Cauchy-Riemannの方程式(正則の必要条件)が成り立たない.よって,
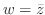 は正則ではない.
は正則ではない.
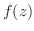 が正則で
が正則で
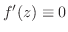 なら,
なら,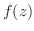 は定数であることを証明せよ.
は定数であることを証明せよ.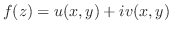 が正則であるから定理3.4によって
が正則であるから定理3.4によって
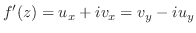
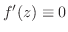 であるから,
であるから,
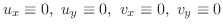 .ゆえに
.ゆえに
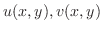 はいずれも定数.したがって,
はいずれも定数.したがって,
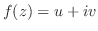 も定数である.
も定数である.
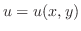 は調和関数であることを示し,これを実部にもつ正則関数
は調和関数であることを示し,これを実部にもつ正則関数
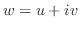 を求めよ.
を求めよ.
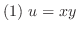
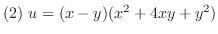
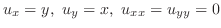 より
より
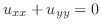 .ゆえに
.ゆえに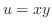 は調和関数.次に,
は調和関数.次に,
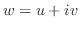 は正則であるからCauchy-Riemannの関係式から
は正則であるからCauchy-Riemannの関係式から
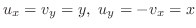
 について積分すると
について積分すると
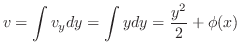
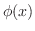 は
は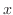 だけの関数である.これをあとの式に代入すると
だけの関数である.これをあとの式に代入すると
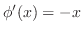 .
よって
.
よって
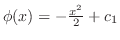 .これより
.これより
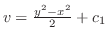 .したがって
.したがって
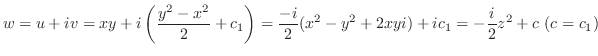
(2)
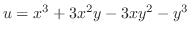 より,
より,
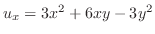 ,
,
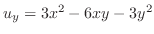 ,
,
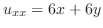 ,
,
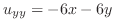 .これより,
.これより,
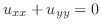 .よって,
.よって,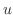 は調和関数.次に,
は調和関数.次に,
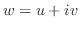 は正則であるからCauchy-Riemannの関係式から
は正則であるからCauchy-Riemannの関係式から
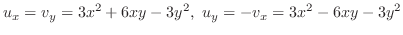
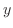 について積分すると
について積分すると
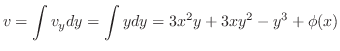
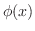 は
は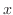 だけの関数である.これをあとの式に代入すると
だけの関数である.これをあとの式に代入すると
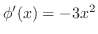 .
よって
.
よって
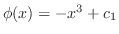 .これより
.これより
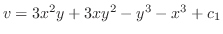 .したがって
.したがって
 |
 |
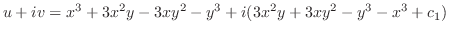 |
|
 |
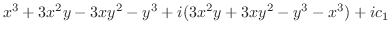 |
||
 |
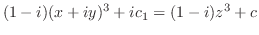 |
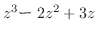
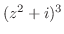
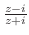
2. 次の関数を微分せよ.
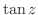
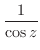
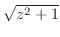
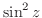
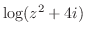
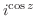
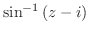
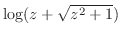
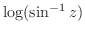
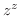
3.
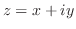 とするとき,次の関数の正則性を調べ,正則ならばその導関数を求めよ.
とするとき,次の関数の正則性を調べ,正則ならばその導関数を求めよ.