Next: コーシー・リーマン関係式(Cauchy-Riemann differential equation) Up: 正則関数(analytic function,holomorphic function) Previous: 正則関数(analytic function,holomorphic function) 索引
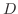 で定義された
で定義された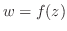 に対し,
に対し,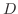 内の点
内の点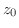 で
で
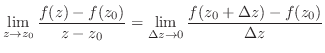
 は
は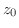 において微分可能(differentiable)であるといい,この極限値を
において微分可能(differentiable)であるといい,この極限値を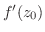 で表わし
で表わし の
の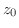 における微分係数(coefficient of derivative)という.
における微分係数(coefficient of derivative)という.
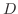 内のすべての
内のすべての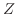 で微分可能なとき,微分係数
で微分可能なとき,微分係数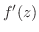 は
は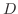 における
における の関数である.これを
の関数である.これを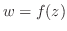 の導関数といい,
の導関数といい,
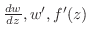 などで表わす.
などで表わす.
(1) 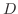 において
において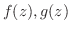 が微分可能ならば次のことが成り立つ
が微分可能ならば次のことが成り立つ
(i)
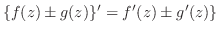
(ii)
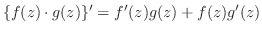
(iii)
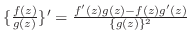
(2) 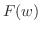 が
が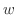 について微分可能,
について微分可能,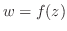 が
が について微分可能ならば,合成関数
について微分可能ならば,合成関数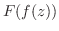 は
は について微分可能で,
について微分可能で,
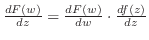 が成り立つ.
が成り立つ.
(3)  が微分可能ならば,
が微分可能ならば, は連続である.
は連続である.