Next: 確認問題詳解 Up: ベクトル積分定理(integral theorems of vector Previous: ベクトル積分定理(integral theorems of vector 索引
(a)
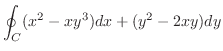 , ただし,
, ただし, 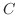 は点
は点
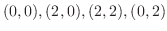 を頂点とする正方形.
を頂点とする正方形.
(b)
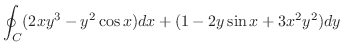 , ただし,
, ただし, 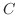 は点
は点 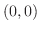 から点
から点
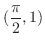 を放物線
を放物線
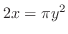 に沿って進む.
に沿って進む.
(c)
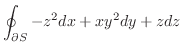 , ただし,
, ただし,
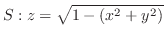
(a)
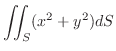 , ただし,
, ただし,
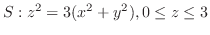
(b)
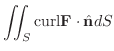 , ただし,
, ただし,
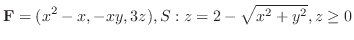
(c)
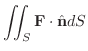 ,
ただし,
,
ただし,
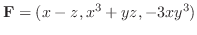 ,
,
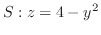 ,
,
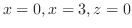
(d)
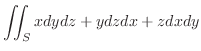 ,
ただし,
,
ただし, 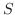 は 円柱
は 円柱
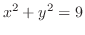 と平面
と平面
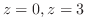 で囲まれた領域
で囲まれた領域
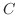 で囲まれた領域の面積
で囲まれた領域の面積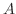 は,
は,
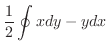 で与えられることを示そう.
で与えられることを示そう.
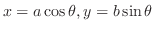 の面積を求めよう.
の面積を求めよう.
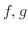 をスカラー場とするとき次の式が成り立つことを示そう.
をスカラー場とするとき次の式が成り立つことを示そう.
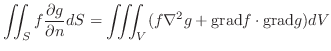 ここで
ここで
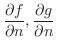 はそれぞれ
はそれぞれ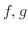 の
の 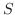 における外向き法線方向の方向微分係数を表わす.
における外向き法線方向の方向微分係数を表わす.