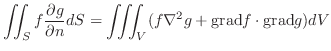Next: 索引 Up: 演習問題詳解 Previous: 8.5 解答 索引
8.6
1. (Greenの定理) 区分的に滑らかな閉曲線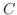 を境界に持つ
を境界に持つ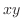 平面上の有界閉領域を
平面上の有界閉領域を とする.また,ベクトル場
とする.また,ベクトル場
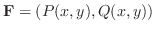 は
は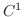 級とする.このとき
級とする.このとき
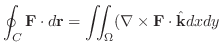
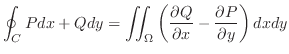
(Stokes の定理)
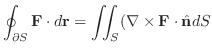
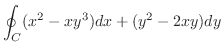 |
 |
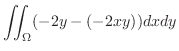 |
|
 |
![$\displaystyle \int_{0}^{2}\int_{0}^{2}(-2y + 2xy)dx dy = \int_{0}^{2}\left[-2xy + x^2 y\right]_{0}^{2} dy$](img5655.png) |
||
 |
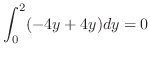 |
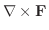 |
 |
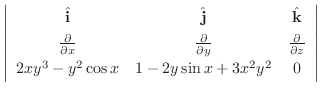 |
|
 |
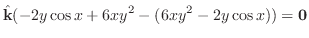 |
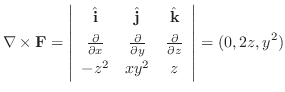
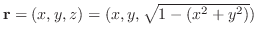 より法線ベクトルを求めると
より法線ベクトルを求めると
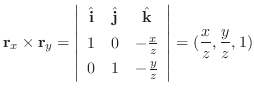
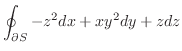 |
 |
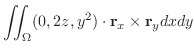 |
|
 |
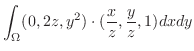 |
||
 |
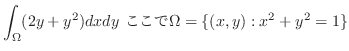 |
||
 |
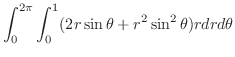 |
||
 |
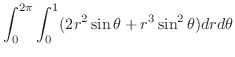 |
||
 |
![$\displaystyle \int_{0}^{2\pi}\left[\frac{2}{3}r^3 \sin{\theta} + \frac{r^4}{4} \sin^{2}{\theta}\right]_{0}^{1}d\theta$](img5671.png) |
||
 |
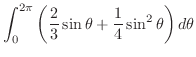 |
||
 |
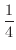 |
2. [Gaussの発散定理]
ベクトル場
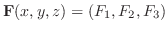 において,区分的に滑らかな閉曲面
において,区分的に滑らかな閉曲面  で囲まれた空間の領域を
で囲まれた空間の領域を 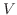 とし,
とし, 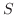 の内部から外部に向かう法線ベクトルを
の内部から外部に向かう法線ベクトルを
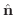 とすると,
とすると,
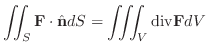
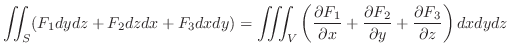
 |
 |
 |
|
 |
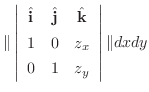 |
||
 |
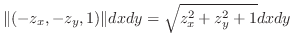 |
||
 |
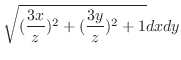 |
||
 |
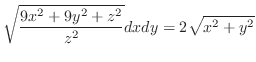 |
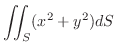 |
 |
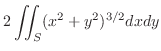 |
|
 |
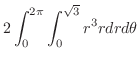 |
||
 |
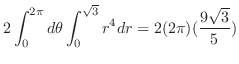 |
||
 |
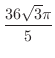 |
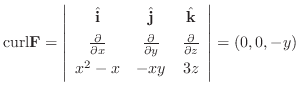
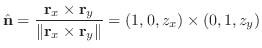
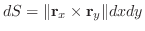
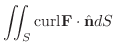 |
 |
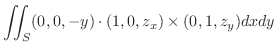 |
|
 |
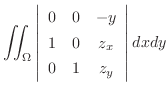 |
||
 |
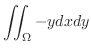 |
||
 |
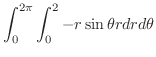 |
||
 |
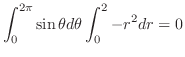 |
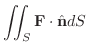 |
 |
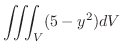 |
|
 |
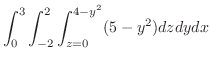 |
||
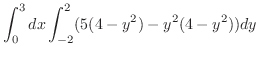 |
|||
 |
![$\displaystyle 6\left[20y - 3y^3 + \frac{y^5}{5}\right]_{0}^{2}$](img5703.png) |
||
 |
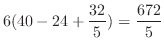 |
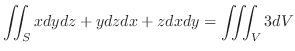
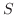 は円柱
は円柱
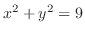 と平面
と平面
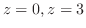 で囲まれた領域なので,その体積は
で囲まれた領域なので,その体積は
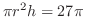 .これより
.これより
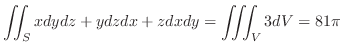
3.
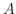 を閉曲線
を閉曲線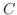 で囲まれた領域とすると,Greenの定理で
で囲まれた領域とすると,Greenの定理で
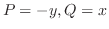 とおくと
とおくと
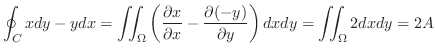
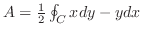
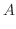 |
 |
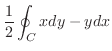 |
|
 |
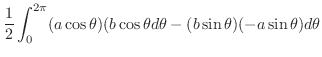 |
||
 |
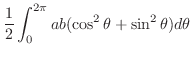 |
||
 |
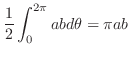 |
5. labelenshU:8-6-5
発散定理において
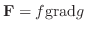 とおくと
とおくと

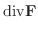 |
 |
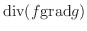 |
|
 |
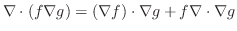 |
||
 |
 |