Next: 8.5 解答 Up: 演習問題詳解 Previous: 8.3 解答 索引
8.4
1.
(a) 点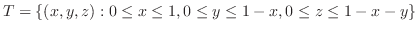 と点
と点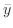 を結ぶ直線をパラメター化し,ベクトル表示すると
を結ぶ直線をパラメター化し,ベクトル表示すると
 の弧長
の弧長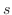 は
は
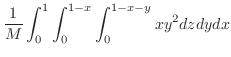
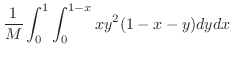 となり,求める線積分は
となり,求める線積分は
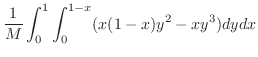 |
 |
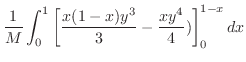 |
|
 |
![$\displaystyle \sqrt{13}\left[\frac{9}{2}t^4 - 3t^3\right]_{0}^{1} = \sqrt{13}(\frac{9}{2} - 3) = \frac{3\sqrt{13}}{2}$](img5394.png) |
(b)
点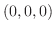 と点
と点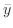 を結ぶ直線をパラメター化し,ベクトル表示すると
を結ぶ直線をパラメター化し,ベクトル表示すると
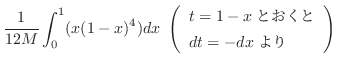
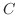 の弧長
の弧長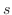 は
は
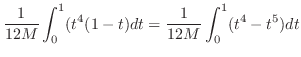
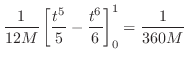 となり,求める線積分は
となり,求める線積分は
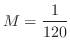 |
 |
![$\displaystyle \sqrt{14}\int_{0}^{1}(t + 9t^2) dt = \sqrt{14}\left[\frac{t^2}{2} + 3t^3\right]_{0}^{1}$](img5399.png) |
|
 |
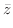 |
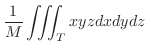
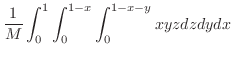 となり
求める線積分は
となり
求める線積分は
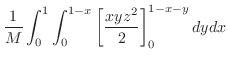 |
 |
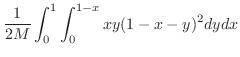 |
|
 |
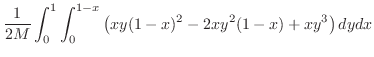 |
||
 |
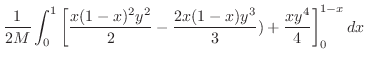 |
(d)
点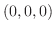 と点
と点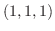 を結ぶ直線
を結ぶ直線 をパラメター化し,ベクトル表示すると
をパラメター化し,ベクトル表示すると
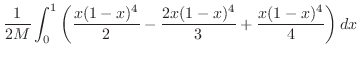
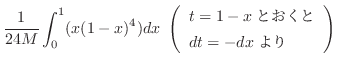 .また,
.また,
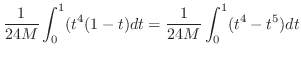 となり
求める線積分は
となり
求める線積分は
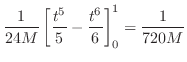 |
 |
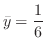 |
|
 |
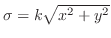 |
||
 |
![$\displaystyle \left[\frac{4t^5 - \frac{11}{3}t^3} + 3t^2\right]_{0}^{1}$](img5413.png) |
||
 |
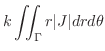 |
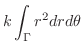
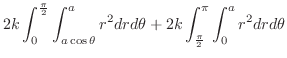 となり
求める線積分は
となり
求める線積分は
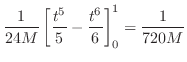 |
 |
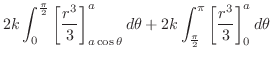 |
|
 |
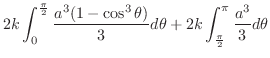 |
||
 |
![$\displaystyle \left[3t^3 - 2t^7 + \frac{20}{13}{t^{13}}\right]_{0}^{1}$](img5419.png) |
||
 |
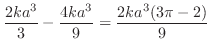 |