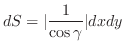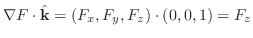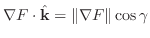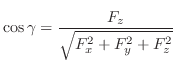Next: 8.2 解答 Up: 演習問題詳解 Previous: 8. ベクトル解析(VECTOR ANALYSIS) 索引
8.1
1.
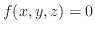 の法ベクトル
の法ベクトル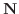 は
は
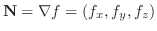
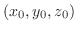 を通り,法ベクトル
を通り,法ベクトル
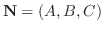 である平面の方程式は,
である平面の方程式は,
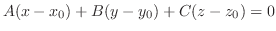
(a)
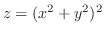 の法ベクトルは
の法ベクトルは
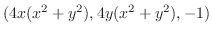 .よって点
.よって点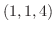 における法ベクトルは
における法ベクトルは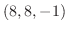 .これより求める平面の方程式は
.これより求める平面の方程式は
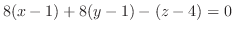
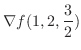 |
 |
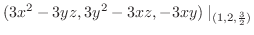 |
|
 |
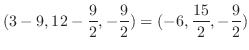 |
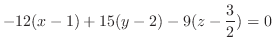
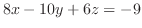
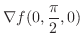 |
 |
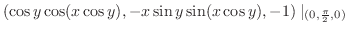 |
|
 |
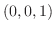 |
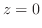
2. 曲面
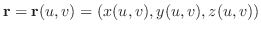 の面積素
の面積素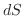 は
は
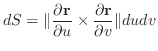
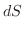 |
 |
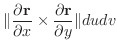 |
|
 |
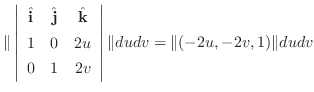 |
||
 |
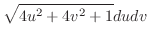 |
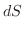 |
 |
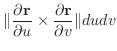 |
|
 |
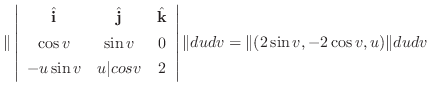 |
||
 |
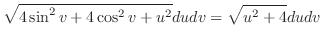 |
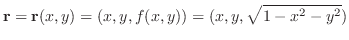
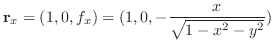
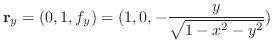
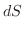 |
 |
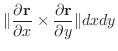 |
|
 |
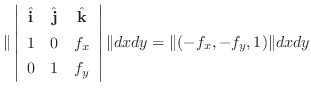 |
||
 |
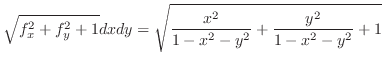 |
||
 |
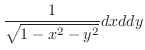 |
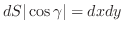
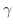 は
は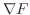 と
と
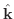 の作る角.これより
の作る角.これより