Next: 7.6 解答 Up: 演習問題詳解 Previous: 7.4 解答 索引
7.5
1.
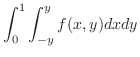
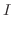 |
 |
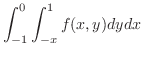 |
|
 |
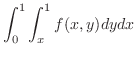 |
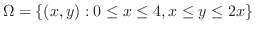 とおくと
とおくと
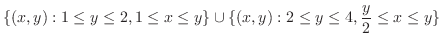
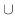
 |
 |
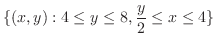 |
|
 |
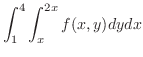 |
||
 |
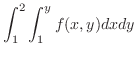 |
||
 |
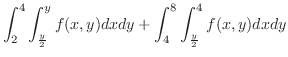 |
(b)
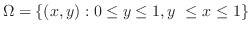 の囲む範囲を求める.その方法として,
の囲む範囲を求める.その方法として,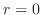 となる角を求めると,
となる角を求めると,
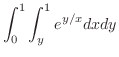 より,
より,
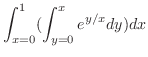 .また,
.また,
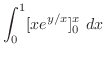 は
は 軸に対称.これより,
軸に対称.これより,
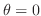 と
と
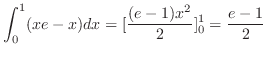 との間の部分の12倍が求める面積となる.
との間の部分の12倍が求める面積となる. を
を
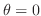 と
と
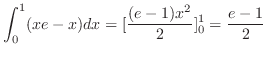 との間とおき,極座標で表わすと
との間とおき,極座標で表わすと は
は
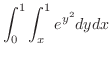
 |
 |
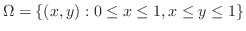 |
|
 |
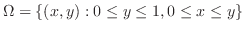 |
||
 |
![$\displaystyle \int_{0}^{\frac{\pi}{6}}\left[\frac{r^2}{2}\right]_{0}^{a\cos{\theta}} d\theta$](img4998.png) |
||
 |
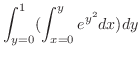 |
||
 |
![$\displaystyle \frac{a^2}{4}\left[\theta + \frac{\sin{6\theta}}{6}\right]_{0}^{\frac{\pi}{6}} = \frac{a^2}{6}(\frac{\pi}{6}) = \frac{a^2 \pi}{24}$](img5000.png) |
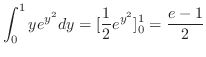
まず,2つの曲線の交点を求めると,
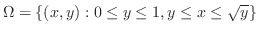
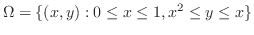 .よって,
.よって,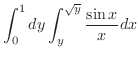 .これよりV-simpleを用いて
.これよりV-simpleを用いて を表わすと
を表わすと
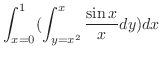
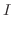 |
 |
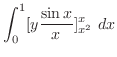 |
|
 |
![$\displaystyle \int_{-2}^{2}\left[y\right]_{\frac{x^2}{4}}^{\frac{8}{x^2 + 4}} dx$](img5007.png) |
||
 |
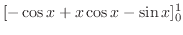 |
||
 |
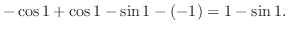 |
||
 |
![$\displaystyle \left[8\cdot\frac{1}{2}\tan^{-1}{\frac{x}{2}} - \frac{x^3}{12}\right]_{-2}^{2}$](img5010.png) |
||
 |
 |
||
 |
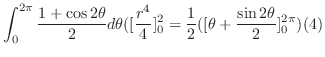 |
2.
(a) 曲面の面積を求めるには,曲面を表わす関数
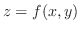 と曲面を正射影してできる
と曲面を正射影してできる が必要となる.
問題より,曲面は
が必要となる.
問題より,曲面は
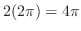 .
.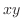 平面への正射影を取ると,つまり,
平面への正射影を取ると,つまり,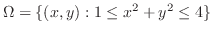 とおくと
とおくと
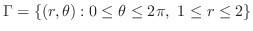
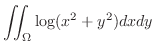
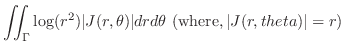
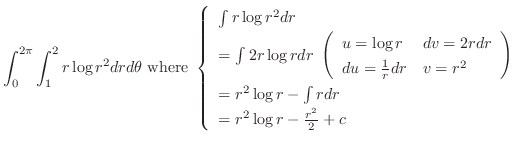

 は円なので,極座標に変換すると
は円なので,極座標に変換すると

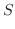 |
 |
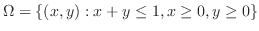 |
|
 |
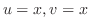 |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}\left[-\sqrt{a^2 - r^2}\right]_{0}^{r} d\theta$](img5023.png) |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}a d\theta = 2a^2 \left[\theta\right]_{0}^{2\pi}$](img5024.png) |
||
 |
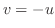 |
(b) 曲面の面積を求めるには,曲面を表わす関数
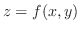 と曲面を正射影してできる
と曲面を正射影してできる が必要となる.
問題より,曲面は
が必要となる.
問題より,曲面は
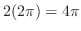 .
.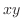 平面への正射影を取ると,つまり,
平面への正射影を取ると,つまり,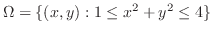 とおくと
とおくと
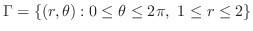
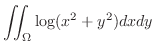
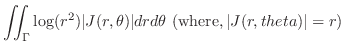
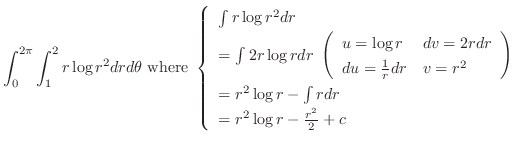


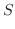 |
 |
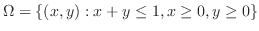 |
|
 |
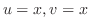 |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}\left[-\sqrt{a^2 - r^2}\right]_{0}^{r} d\theta$](img5023.png) |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}a d\theta = 2a^2 \left[\theta\right]_{0}^{2\pi}$](img5024.png) |
||
 |
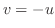 |
(c) 曲面の面積を求めるには,曲面を表わす関数
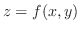 と曲面を正射影してできる
と曲面を正射影してできる が必要となる.
この問題では,
が必要となる.
この問題では,
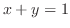 で切り取るので,切り取られた曲面の
で切り取るので,切り取られた曲面の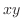 平面への正射影は
平面への正射影は
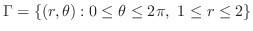
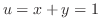 より
より
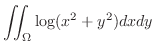
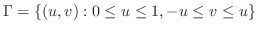
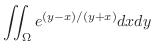
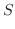 |
 |
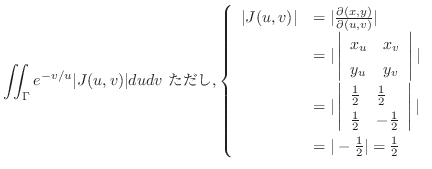 |
|
 |
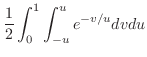 |
||
 |
![$\displaystyle 2\int_{-a}^{a}\left[\frac{ay}{\sqrt{a^2 - x^2}}\right]_{-\sqrt{a^2 - x^2}}^{\sqrt{a^2 - x^2}} dx$](img5032.png) |
||
 |
![$\displaystyle 4\int_{-a}^{a}a dx = 8a\int_{0}^{a} dx = 8a[x]_{0}^{a} = 8a^2$](img5033.png) |
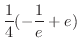
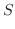 |
 |
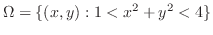 |
|
 |
![$\displaystyle 2\pi m \sqrt{1 + m^2}[x]_{0}^{k} = \pi m \sqrt{1 + m^2} k^2$](img5037.png) |
3. 有界閉領域 上で連続な関数
上で連続な関数
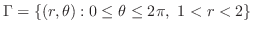 が与えられたとき,
が与えられたとき, の境界
の境界
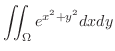 を通り
を通り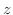 軸に平行な直線群と
軸に平行な直線群と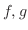 のグラフ曲面で囲まれた立体の体積は
のグラフ曲面で囲まれた立体の体積は

(a) 問題より求める立体は
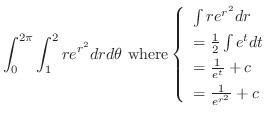 の境界を通り
の境界を通り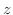 軸に平行な直線群と関数
軸に平行な直線群と関数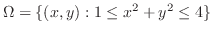 ,
,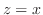 のグラフで囲まれている.
のグラフで囲まれている. を極座標に変換すると,
を極座標に変換すると,
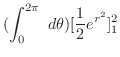 より
より
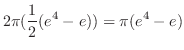
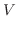 |
 |
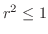 |
|
 |
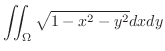 |
||
 |
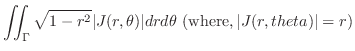 |
||
 |
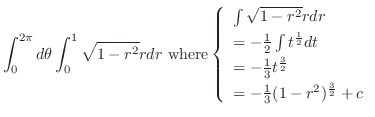 |
||
 |
![$\displaystyle 2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^3}{3}\right]_{0}^{a}$](img5048.png) |
||
 |
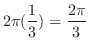 |
(b) 問題より求める立体は
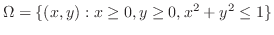 の境界を通り
の境界を通り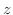 軸に平行な直線群と関数
軸に平行な直線群と関数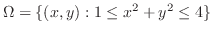 ,
,
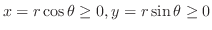 で囲まれている.H-simpleを用いて
で囲まれている.H-simpleを用いて を表わすと
を表わすと
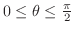
 |
 |
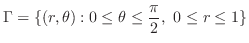 |
|
 |
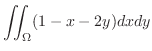 |
||
 |
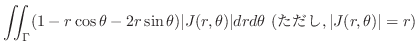 |
||
 |
![$\displaystyle \int_{0}^{1}\left[x - \frac{x^3}{3}\right]_{0}^{1 - y^2} dy$](img5056.png) |
||
 |
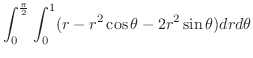 |
||
 |
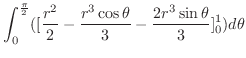 |
||
 |
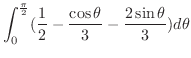 |
||
 |
![$\displaystyle \left[\frac{2}{3}y - \frac{y^5}{5} + \frac{1}{21}y^7\right]_{0}^{1}$](img5060.png) |
||
 |
 |
(c) 問題より求める立体は
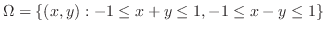 の境界を通り
の境界を通り 軸に平行な直線群と関数
軸に平行な直線群と関数
 ,
,
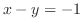 で囲まれている.極座標を用いて
で囲まれている.極座標を用いて の境界を表わすと
の境界を表わすと
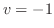 より
より
 .よって,
.よって,
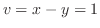 が0になるのは,
が0になるのは,
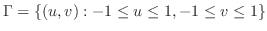 .これより
.これより
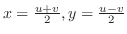
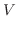 |
 |
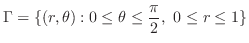 |
|
 |
 |
||
 |
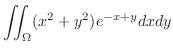 |
||
 |
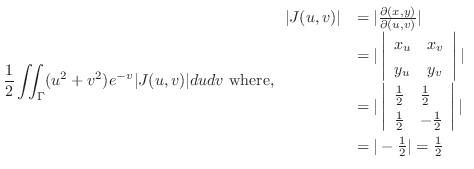 |
||
 |
![$\displaystyle 4\int_{0}^{\frac{\pi}{2}}\left[-\frac{1}{3}(a^2 - r^2)^{\frac{3}{2}}\right]_{0}^{a\cos{\theta}} d\theta$](img5073.png) |
||
 |
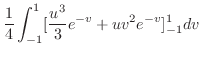 |
||
 |
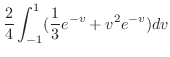 |
||
 |
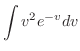 |
||
 |
 |
(d)
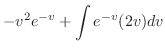 と平面
と平面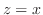 の交線は,
の交線は,
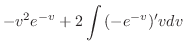 .よって,求める立体は
.よって,求める立体は
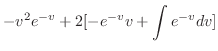 の境界を通り
の境界を通り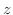 軸に平行な直線群と関数
軸に平行な直線群と関数
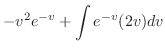 ,
,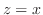 で囲まれている.極座標を用いて
で囲まれている.極座標を用いて の境界を表わすと
の境界を表わすと
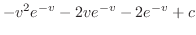 より
より
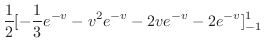 .
.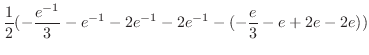 より,
より,
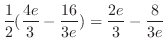 .よって,
.よって,
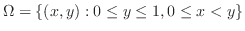 .これより,
.これより,
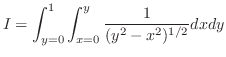
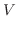 |
 |
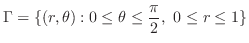 |
|
 |
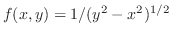 |
||
 |
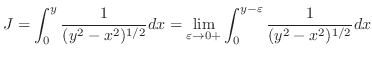 |
||
 |
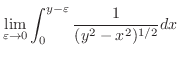 |
||
 |
![$\displaystyle 2\int_{0}^{\frac{\pi}{2}}\left[\frac{r^2}{2} - \frac{r^3}{3}(1 + \cos{\theta})\right]_{0}^{\frac{1}{1 + \cos{\theta}}} d\theta$](img5090.png) |
||
 |
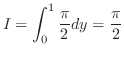 |
||
 |
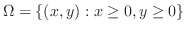 |
||
 |
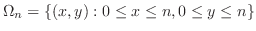 |
||
 |
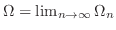 |
||
 |
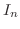 |
||
 |
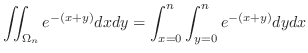 |
||
 |
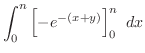 |
||
 |
![$\displaystyle \frac{1}{6}\left[t + \frac{t^3}{3}\right]_{0}^{1}$](img5098.png) |
||
 |
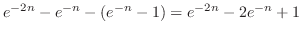 |