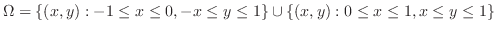Next: 7.5 解答 Up: 演習問題詳解 Previous: 7.3 解答 索引
7.4
1.
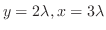
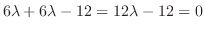
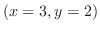 は
は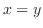 で定義されないので,
で定義されないので,
 |
 |
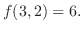 |
|
 |
![$\displaystyle \lim_{\varepsilon \to 0}[\sin^{-1}{x}{y}]_{0}^{y - \varepsilon} = \frac{\pi}{2}$](img4925.png) |
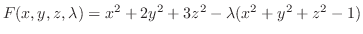
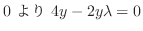
 より
より
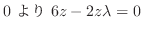 |
 |
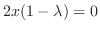 |
|
 |
![$\displaystyle \int_{0}^{n}\left[-e^{-(x+y)}\right]_{0}^{n} \ dx$](img4932.png) |
||
 |
![$\displaystyle \int_{0}^{n}(-e^{(x+n)} + e^{-x})dx = \left[e^{-(x+n)} + e^{-x}\right]_{0}^{n}$](img4933.png) |
||
 |
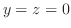 |
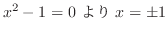
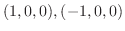 は有界.
は有界.
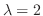 は
は
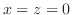 で有界.そこで,
で有界.そこで,
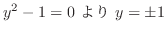
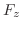 より
より
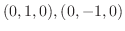
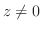
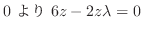 |
 |
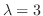 |
|
 |
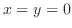 |
||
 |
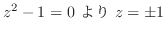 |
||
 |
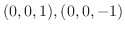 |
||
 |
![$\displaystyle \left[\frac{\theta^2}{2}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^...
...\right]_{\frac{\sqrt{2}}{n}}^{1} = \frac{\pi^2}{8}(\frac{1}{2} - \frac{1}{n^2})$](img4946.png) |
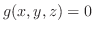
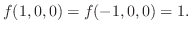
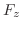 より
より
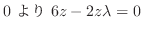 |
 |
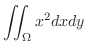 |
|
 |
![$\displaystyle \int_{1}^{n}\left[-\frac{1}{x^2 y}\right]_{1}^{n} \ dx$](img4951.png) |
||
 |
![$\displaystyle \int_{1}^{n}(\frac{1}{x^2} - \frac{1}{x^2 n})dx = \left[-\frac{1}{x} + \frac{1}{xn}\right]_{1}^{n}$](img4952.png) |
||
 |
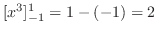 |
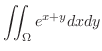
(e)
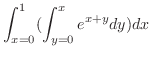 は曲線
は曲線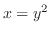 上で定義されない.そこで,
上で定義されない.そこで,
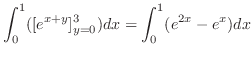 を除いた集合を
を除いた集合を
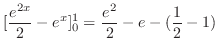 とする.H-simpleを用いると
とする.H-simpleを用いると
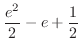
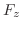 より
より
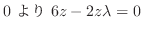 |
 |
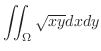 |
|
 |
![$\displaystyle \int_{-\sqrt{1 - \frac{1}{n}}}^{\sqrt{1 - \frac{1}{n}}}\left[2\sqrt{x - y^2}\right]_{y^2 + \frac{1}{n}}^{1} \ dy$](img4960.png) |
||
 |
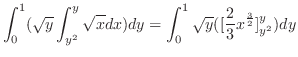 |
||
 |
![$\displaystyle 2(\frac{1}{2}) \left[\sqrt{1 - y^2} + \sin^{-1}{y} - \sqrt{\frac{1}{n}} y\right]_{-\sqrt{1 - \frac{1}{n}}}^{\sqrt{1 - \frac{1}{n}}}$](img4962.png) |
||
 |
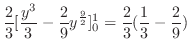 |
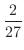
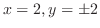
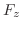 .極座標変換をすると
.極座標変換をすると
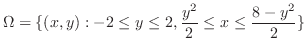
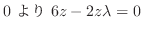 |
 |
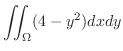 |
|
 |
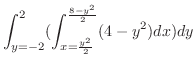 |
||
 |
![$\displaystyle \int_{0}^{2\pi} d\theta\left[\frac{1}{2}\tan^{-1}{r^2}\right]_{0}^{2\pi}$](img4970.png) |
||
 |
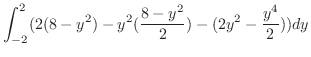 |
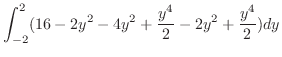
2.
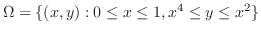
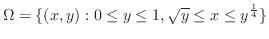 とおくと,
とおくと,
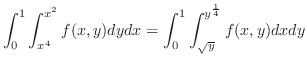
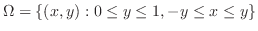 より
より