Next: 7.3 解答 Up: 演習問題詳解 Previous: 7. 重積分法(MULTIPLE INTEGRATION) 索引
7.2
1. 積分の領域を,V-simpleまたはH-simpleで表わす.
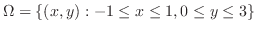
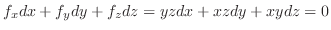 |
 |
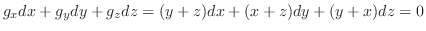 |
|
 |
![$\displaystyle \int_{-1}^{1}([x^2 y]_{y=0}^{3})dx = \int_{-1}^{1}3x^2 dx$](img4787.png) |
||
 |
![$\displaystyle [x^3]_{-1}^{1} = 1 - (-1) = 2$](img4788.png) |
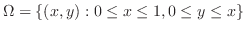
 |
 |
 |
|
 |
![$\displaystyle \int_{0}^{1}([e^{x+y}]_{y=0}^{3})dx = \int_{0}^{1}(e^{2x} - e^{x}) dx$](img4791.png) |
||
 |
![$\displaystyle [\frac{e^{2x}}{2} - e^{x}]_{0}^{1} = \frac{e^{2}}{2} - e -(\frac{1}{2} - 1)$](img4792.png) |
||
 |
 |
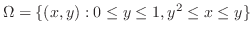
 |
 |
 |
|
 |
![$\displaystyle \int_{0}^{1}(\sqrt{y}\int_{y^2}^{y}\sqrt{x} dx)dy = \int_{0}^{1}\sqrt{y}([\frac{2}{3}x^{\frac{3}{2}}]_{y^2}^{y} ) dy$](img4796.png) |
||
 |
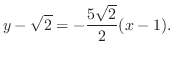 |
||
 |
![$\displaystyle \frac{2}{3}[\frac{y^3}{3} - \frac{2}{9}y^{\frac{9}{2}}]_{0}^{1} = \frac{2}{3}(\frac{1}{3} - \frac{2}{9})$](img4798.png) |
||
 |
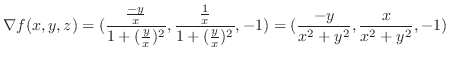 |
(d)
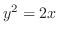 と
と
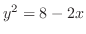 の交点を求めると,
の交点を求めると,
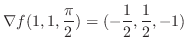 より
より
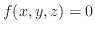 となる.そこでH-simpleを用いると
となる.そこでH-simpleを用いると
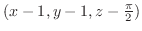
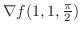 |
 |
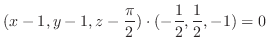 |
|
 |
![$\displaystyle \int_{-2}^{2}([4x - y^2 x]_{\frac{y^2}{2}}^{\frac{8 - y^2}{2}} )dy$](img4805.png) |
||
 |
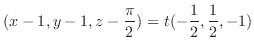 |
||
 |
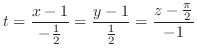 |
||
 |
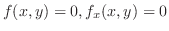 |
||
 |
![$\displaystyle 2[\frac{y^5}{5} - \frac{8y^3}{3} + 16y]_{0}^{2} = 2(\frac{256}{15}) = \frac{512}{15}.$](img4809.png) |
2.
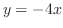
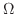 をH-simpleで表わすと
をH-simpleで表わすと
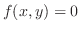
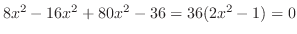
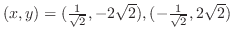
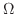 をV-simpleで表わすと
をV-simpleで表わすと
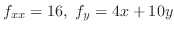
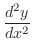 |
 |
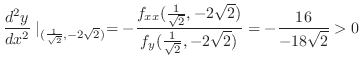 |
|
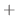 |
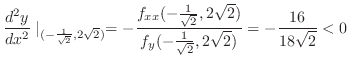 |
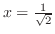
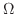 をH-simpleで表わすと
をH-simpleで表わすと
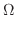 |
 |
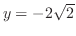 |
|
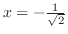 |
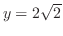 |
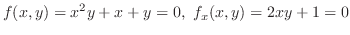 |
 |
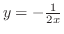 |
|
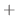 |
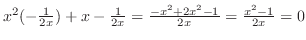 |
3.
(a)
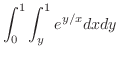 をこのまま積分できない.そこで,積分順序の交換を行なう.
をこのまま積分できない.そこで,積分順序の交換を行なう.
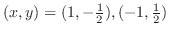
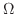 をV-simpleで表わすと
をV-simpleで表わすと
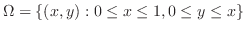
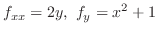 |
 |
 |
|
 |
![$\displaystyle \int_{0}^{1}[xe^{y/x}]_{0}^{x} \ dx$](img4828.png) |
||
 |
![$\displaystyle \int_{0}^{1}(xe - x)dx = [\frac{(e-1)x^2}{2}]_{0}^{1} = \frac{e-1}{2}$](img4829.png) |
(b)
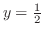 をこのまま積分できない.そこで,積分順序の交換を行なう.
をこのまま積分できない.そこで,積分順序の交換を行なう.
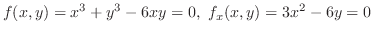
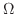 をH-simpleで表わすと
をH-simpleで表わすと
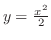
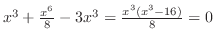 |
 |
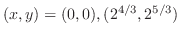 |
|
 |
![$\displaystyle \int_{0}^{1}[xe^{y^{2}}]_{0}^{y} \ dy$](img4835.png) |
||
 |
![$\displaystyle \int_{0}^{1}ye^{y^{2}} dy = [\frac{1}{2}e^{y^2}]_{0}^{1} = \frac{e-1}{2}$](img4836.png) |
(c)
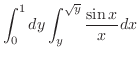 をこのまま積分できない.そこで,積分順序の交換を行なう.
をこのまま積分できない.そこで,積分順序の交換を行なう.
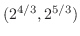
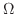 をV-simpleで表わすと
をV-simpleで表わすと
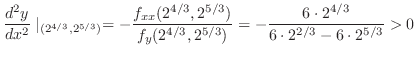
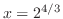 |
 |
 |
|
 |
![$\displaystyle \int_{0}^{1}[y\frac{\sin{x}}{x}]_{x^2}^{x} \ dx$](img4841.png) |
||
 |
 |
||
 |
![$\displaystyle [-\cos{x} + x\cos{x} - \sin{x}]_{0}^{1}$](img4843.png) |
||
 |
 |