Next: 7. 重積分法(MULTIPLE INTEGRATION) Up: 演習問題詳解 Previous: 6.8 解答 索引
6.9
1.
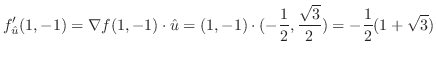 より定まる陰関数
より定まる陰関数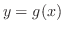 が
が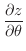 で極値
で極値
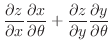 をとるならば,
をとるならば,
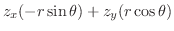
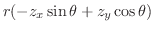
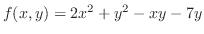
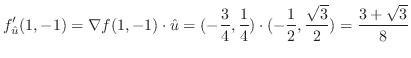
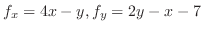 .
次に,
.
次に,
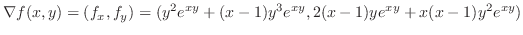
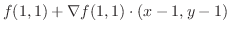 を計算すると
を計算すると
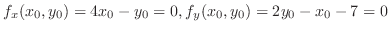
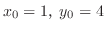
よって
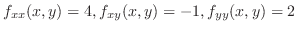 のとき
のとき
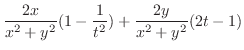 は極小値,
は極小値,
 のとき
のとき
 は極大値.
は極大値.
まず,
 を満たす
を満たす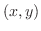 を求める.
を求める.
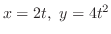
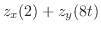 .これを
.これを
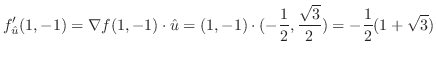 に代入すると
に代入すると
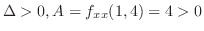
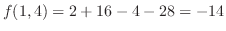 .
次に,
.
次に,
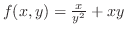
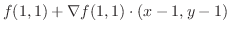 を計算すると
を計算すると
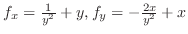
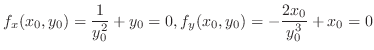
よって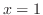 のとき
のとき
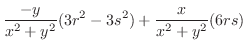 は極小値,
は極小値,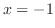 のとき
のとき
 も極小値.
も極小値.
まず,
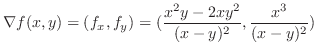 を満たす
を満たす を求める.
を求める.
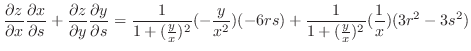
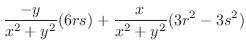 .これを
.これを
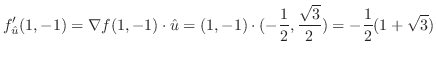 に代入すると
に代入すると
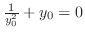
![$(0,0), (2\sqrt[3]{2}, 2\cdot2^{\frac{2}{3}})$](img4692.png) .
次に,
.
次に,
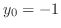
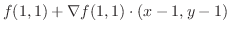 を計算すると
を計算すると
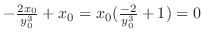
![$\displaystyle \frac{d^2 y}{dx^2}\mid_{(2\sqrt[3]{2}, 2\cdot2^{\frac{2}{3}})} = -\frac{6\cdot 2\sqrt[3]{2}}{-6} > 0$](img4695.png)
よって
![$x = 2\sqrt[3]{2}$](img4696.png) のとき
のとき
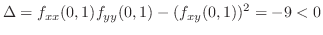 は極小値.
は極小値.
2.
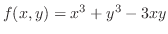 と
と
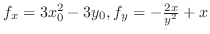 の少なくとも一方は0でないとする.
条件
の少なくとも一方は0でないとする.
条件
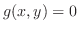 の元で,
の元で,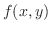 が
が
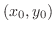 で極値をとるための必要条件は
で極値をとるための必要条件は
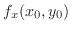
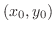 で
で
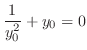
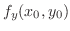 の点を特異点という.
の点を特異点という.
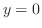 のとき式(10.9)より,
のとき式(10.9)より,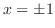 ,式(10.10)より
,式(10.10)より
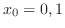 .
.
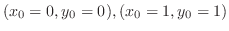 のとき,式(10.11)より
のとき,式(10.11)より
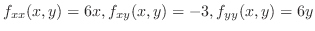 .式(10.10)に代入して,
.式(10.10)に代入して,
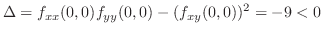 より
より
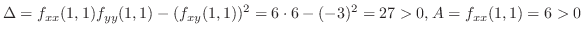 .式(10.9)に代入して
.式(10.9)に代入して
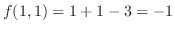 より
より
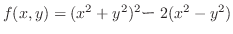 .よって,
.よって,
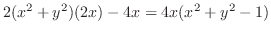 .したがって,式(10.9),(10.10),(10.11)の解は,
.したがって,式(10.9),(10.10),(10.11)の解は,
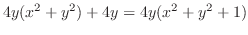
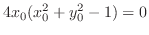 の値は,
の値は,
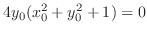
 は有界閉集合で,この上で
は有界閉集合で,この上で は連続だから最大値,最小値を持つ.以上より,最大値は
は連続だから最大値,最小値を持つ.以上より,最大値は
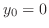
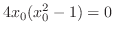
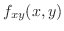
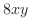
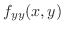
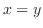 ,または,
,または,
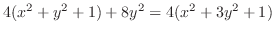 .
.
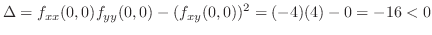 より
より
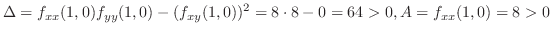 .したがって,
.したがって,
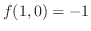 .
一方,
.
一方,
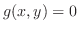 の第1象限の部分に原点をつけ加えたものは有界閉曲線で,
の第1象限の部分に原点をつけ加えたものは有界閉曲線で, はその上で連続だから最大値,最小値を持つ.以上より,最大値は
はその上で連続だから最大値,最小値を持つ.以上より,最大値は
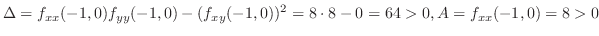
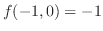 なら
なら
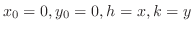 であるから,
であるから,
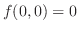 が極小値かつ最小値である.
が極小値かつ最小値である.
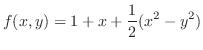
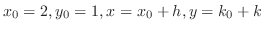
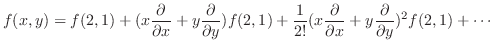
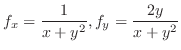 .
.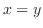 のとき
のとき
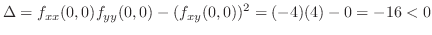 より
より
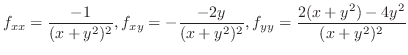 .したがって,
.したがって,
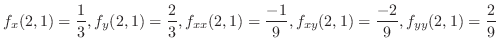 .
.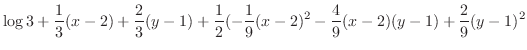 のとき
のとき
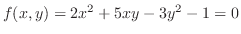 .したがって,
.したがって,
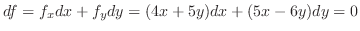 .
このとき,
.
このとき,
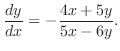 の値は,
の値は,
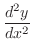
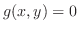 は有界閉集合で,この上で
は有界閉集合で,この上で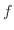 は連続だから最大値,最小値を持つ.以上より,最大値は
は連続だから最大値,最小値を持つ.以上より,最大値は
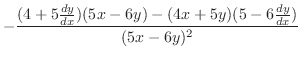
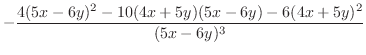
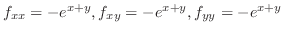 .これを式(10.18)に代入すると
.これを式(10.18)に代入すると
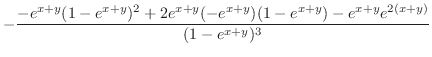
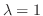 より
より
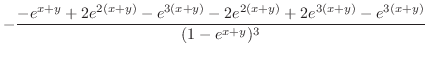 .一方,
.一方,
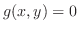 は有界閉集合ではないが,
は有界閉集合ではないが,
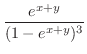 とすると,
とすると,
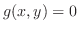 は有界閉集合となり,この上で
は有界閉集合となり,この上で
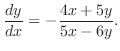 は最大値を持つ.以上より,最大値は
は最大値を持つ.以上より,最大値は
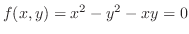
4.
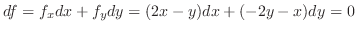 とおくと
とおくと
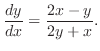 .
.
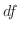 ,
,
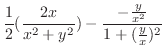 ,
,
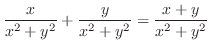 .ここで,
.ここで,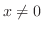 とすると,
とすると,
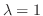 より
より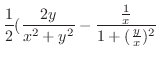 .これを式(10.21)に代入すると
.これを式(10.21)に代入すると
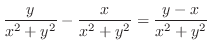
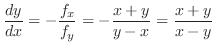 .
.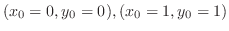 とすると,
とすると,
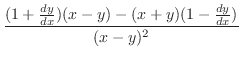 より
より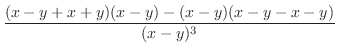 .これを式(10.21)に代入すると
.これを式(10.21)に代入すると
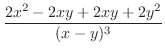
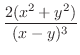 .
.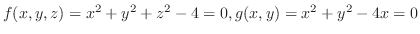 とすると,
とすると,
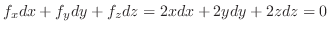 より
より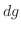 .これを式(10.21)に代入すると
.これを式(10.21)に代入すると
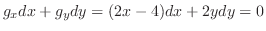
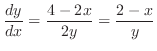 .これより式(10.21)の値を求めると
.これより式(10.21)の値を求めると
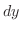
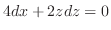 は有界閉集合で,この上で
は有界閉集合で,この上で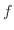 は連続だから最大値,最小値を持つ.以上より,最大値は
は連続だから最大値,最小値を持つ.以上より,最大値は