Next: 6.2 解答 Up: 演習問題詳解 Previous: 6. 偏微分法(PARTIAL DIFFERENTIATION) 索引
6.1
1.
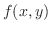 の定義域とは関数
の定義域とは関数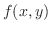 が実数の値をとる
が実数の値をとる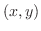 の範囲のことである.
の範囲のことである.
2変数関数のグラフは正面図(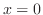 ),側面図(
),側面図(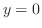 ),等位面(
),等位面(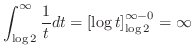 )を用いて描く.
(a)
)を用いて描く.
(a)
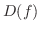 |
 |
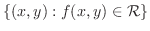 |
|
 |
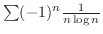 |
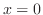 とおくと,
とおくと,
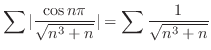 より
より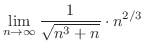 平面に放物線.
平面に放物線.
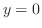 とおくと,
とおくと,
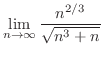 より
より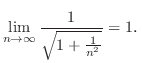 平面に放物線.
平面に放物線.
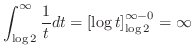 とおくと,
とおくと,
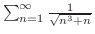 より,等位面
より,等位面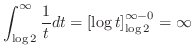 に双曲線となる.これを用いて図を描く.
に双曲線となる.これを用いて図を描く.
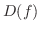 |
 |
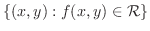 |
|
 |
 |
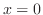 とおくと,
とおくと,
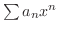 .
.
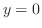 とおくと,
とおくと,
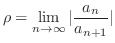 より
より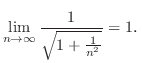 平面に直線.
平面に直線.
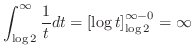 とおくと,
とおくと,
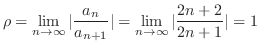 より,
より,
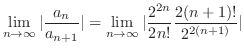 .
.
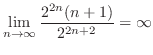 より
より
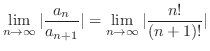
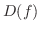 |
 |
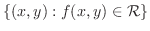 |
|
 |
 |
||
 |
 |
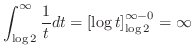 とおくと,
とおくと,
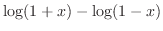 より,
より,
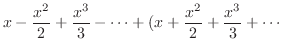 .
.
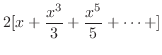 .ここで,
.ここで,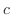 の値を変化させながらグラフを描く
の値を変化させながらグラフを描く