4.3 解答

4.3

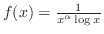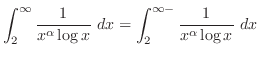1. 交項級数 $\sum (-1)^{n}a_{n}$ において， $a_{1} \geq a_{2} \geq a_{3} \geq \cdots \geq a_{n} \geq$ で

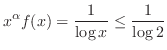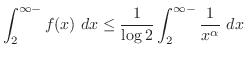$\displaystyle \lim_{n \to \infty}{a_{n}} = 0 \$ ならば $\displaystyle ，\sum (-1)^{n}a_{n}$ は収束

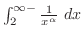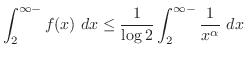$\displaystyle \sum a_{n} < \infty$ ならば $\displaystyle ，\sum (-1)^{n}a_{n}$ は絶対収束

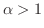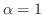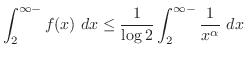$\displaystyle \sum (-1)^{n}a_{n} < \infty$ で $\displaystyle \ \sum a_{n} = \infty$ ならば $\displaystyle ，\sum (-1)^{n}a_{n}$ は条件収束

(a) 数列 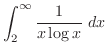$\{a_{n}\} = \{\frac{\log{n}}{n}\}$ は単調減少数列で 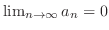$\lim_{n \to \infty}a_{n} = 0$ よって収束．次に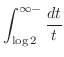， $\sum \frac{\log{n}}{n}$ について調べる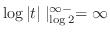． $f(x) = \frac{\log{x}}{x}$ とおくと

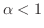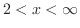$\displaystyle \int_{1}^{\infty}f(x) dx$	$\displaystyle =$	$\displaystyle \int_{1}^{\infty}\frac{\log{x}}{x}dx \ \left(t = \log{x}, dt = \frac{1}{x}dx\right)$
	$\displaystyle =$	$\displaystyle \int_{0}^{\infty}tdt = \left[\frac{t^2}{2}\right]_{1}^{\infty-0} = \infty$

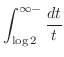よって，積分判定法により $\sum \frac{\log{n}}{n}$ は発散．したがって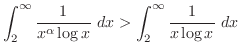， $\sum (-1)^{n}\frac{\log{n}}{n}$ は条件収束．

(b) $\sum \frac{n}{3^{n}}$ について考える．

$\displaystyle \lim_{n \to \infty}\frac{a_{n+1}}{a_{n}}$	$\displaystyle =$	$\displaystyle \lim_{n \to \infty}\frac{n+1}{3^{n+1}}\cdot\frac{3^{n}}{n}$
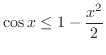	$\displaystyle =$	$\displaystyle \lim_{n \to \infty}\frac{n+1}{3n} = \frac{1}{3} < 1$

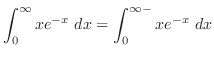より $\sum_{n=1}^{\infty}\frac{n}{3^{n}}$ は収束．したがって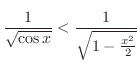， $\sum_{n=1}^{\infty}(-1)^{n}\frac{n}{3^{n}}$ は絶対収束．

(c)

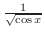
$\displaystyle \sum (\frac{1}{\sqrt{n}} - \frac{1}{\sqrt{n+1}}) = \sum \frac{\sq... ... \sqrt{n}}{\sqrt{n(n+1)}} = \sum \frac{1}{\sqrt{n(n+1)}(\sqrt{n+1} + \sqrt{n})}$

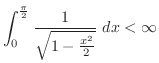より $\sum \frac{1}{n^{3/2}} < \infty$ と比較する．比較判定法を用いると

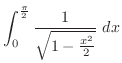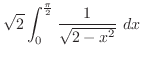$\displaystyle \lim_{n \to \infty}\frac{1}{\sqrt{n(n+1)}(\sqrt{n+1} + \sqrt{n})}\cdot n^{2/3}$	$\displaystyle =$	$\displaystyle \lim_{n \to \infty}\frac{n^{2/3}}{n\sqrt{1+\frac{1}{n}}(\sqrt{n}(\sqrt{1+\frac{1}{n}} + 1))}$
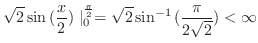	$\displaystyle =$	$\displaystyle \lim_{n \to \infty}\frac{1}{\sqrt{1 + \frac{1}{n}}(\sqrt{1 + \frac{1}{n}} + 1)} = \frac{1}{2} < 1．$

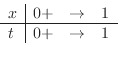したがって， $\sum_{n=1}^{\infty}(\frac{1}{\sqrt{n}} - \frac{1}{\sqrt{n+1}})$ は収束．

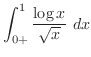(d) 数列 $\{a_{n}\} = \{\frac{1}{2n-1}\}$ は単調減少数列で 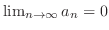$\lim_{n \to \infty}a_{n} = 0$ よって収束．次に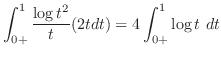， $\sum \frac{1}{2n-1}$ について調べる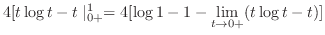． $\sum \frac{1}{n} = \infty$ を用いて比較すると，

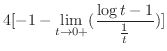
$\displaystyle \lim_{n \to \infty}\frac{1}{2n-1}\cdot n = \lim_{n \to \infty}\frac{n}{2n-1} = \frac{1}{2}$

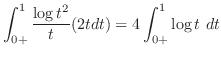よって，比較判定法により $\sum \frac{1}{2n-1}$ は発散．したがって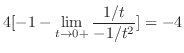， $\sum (-1)^{n}\frac{1}{2n-1}$ は条件収束．

(e) 数列 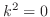$\{a_{n}\} = \{\frac{1}{n\log{n}}\}$ は単調減少数列で 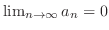$\lim_{n \to \infty}a_{n} = 0$ よって収束．次に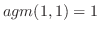， $\sum \frac{1}{n\log{n}}$ について調べる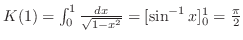． $f(x) = \frac{1}{x\log{x}}$ とおくと

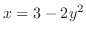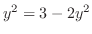$\displaystyle \int_{2}^{\infty}f(x) dx$	$\displaystyle =$	$\displaystyle \int_{1}^{\infty}\frac{2}{x\log{x}}dx \ \left(t = \log{x}, dt = \frac{1}{x}dx\right)$
	$\displaystyle =$	$\displaystyle \int_{\log{2}}^{\infty}\frac{1}{t}dt = \left[\log{t}\right]_{\log{2}}^{\infty-0} = \infty$

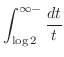よって，積分判定法により $\sum \frac{\log{n}}{n}$ は発散．したがって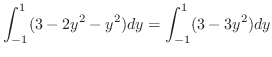， $\sum (-1)^{n}\frac{1}{n\log{n}}$ は条件収束．

(f)

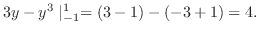
$\displaystyle \sum \vert\frac{\cos{n\pi}}{\sqrt{n^3 + n}}\vert = \sum \frac{1}{\sqrt{n^3 + n}}$

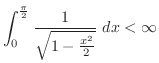より $\sum \frac{1}{n^{3/2}} < \infty$ と比較する．比較判定法を用いると

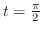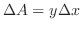$\displaystyle \lim_{n \to \infty}\frac{1}{\sqrt{n^3 + n}}\cdot n^{2/3}$	$\displaystyle =$	$\displaystyle \lim_{n \to \infty}\frac{n^{2/3}}{\sqrt{n^3 + n}}$
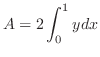	$\displaystyle =$	$\displaystyle \lim_{n \to \infty}\frac{1}{\sqrt{1 + \frac{1}{n^2}}} = 1．$

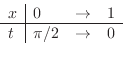したがって， $\sum_{n=1}^{\infty}\frac{1}{\sqrt{n^3 + n}}$ は収束．つまり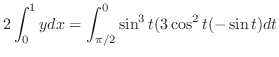， $\sum \frac{\cos{n\pi}}{\sqrt{n^3 + n}}$ は絶対収束．