Next: 広義積分(improper integrals) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 累次積分(repeated integrals) 目次 索引
1変数関数  の定積分に関する置換積分の公式に対応するものを2重積分で考えてみましょう.
の定積分に関する置換積分の公式に対応するものを2重積分で考えてみましょう.
いま 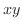 平面上の領域
平面上の領域  と
と 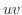 平面上の領域
平面上の領域 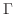 との間に
との間に
 |
 |
 |
|
 |
 |
 |
 があり,
があり,  は
は 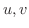 に関して
に関して 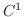 級であるとします.さらに,
級であるとします.さらに,

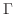 上で常に0にならないものとします.このとき次の定理が成り立ちます.
上で常に0にならないものとします.このとき次の定理が成り立ちます.
 上で連続な関数
上で連続な関数 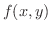 に対して次の式が成り立つ.
に対して次の式が成り立つ.

ここで用いられた  を ジャコビアン(Jacobian) といいます.簡単な例でジャコビアンを説明しましょう.
を ジャコビアン(Jacobian) といいます.簡単な例でジャコビアンを説明しましょう.
例えば, が
が
 で与えられたとします.すると,
で与えられたとします.すると,

 が正則行列ならば,逆行列
が正則行列ならば,逆行列  が存在するので,
が存在するので,

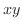 平面上に4点
平面上に4点
 を頂点とする長方形を考えます.この長方形の面積は
を頂点とする長方形を考えます.この長方形の面積は
 で与えられることに注意し,対応する
で与えられることに注意し,対応する 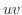 平面上の図形の面積を求めてみましょう.
平面上の図形の面積を求めてみましょう.
 より
より

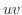 平面上の図形の面積
平面上の図形の面積
 は
は


特に極座標
 を直交座標
を直交座標 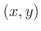 に変換するときは,
に変換するときは,
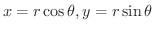 より,
より,



解
極座標変換を用いると,
 , また,
, また,
 より
より
 .よって
.よって  は
は

 |
 |
 |
|
 |
![$\displaystyle \int_{0}^{1}r^{3}dr\int_{0}^{\frac{\pi}{2}}\sin{\theta}\cos{\thet...
...heta}}{2}\right ]_{0}^{\frac{\pi}{2}} = \frac{1}{8}
\ensuremath{\ \blacksquare}$](img3970.png) |
 のとき,2重積分
のとき,2重積分

解
極座標変換を用いると
 より
より  は
は

 |
 |
 |
|
 |
![$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left[-\frac{1}{3}(1-r^2)^{3/2}\right ]_{0}^{\cos{\theta}} d{\theta}$](img3976.png) |
||
 |
 |
 重積分を計算しよう.
重積分を計算しよう.
 とおくと,領域
とおくと,領域
 はどんな図形に移されるか図示せよ.また,この変数変換を用いて,2重積分
はどんな図形に移されるか図示せよ.また,この変数変換を用いて,2重積分
 の値を求めよう.
の値を求めよう.
 とするとき,2重積分
とするとき,2重積分
 の値を求めよう
の値を求めよう