Next: 累次積分(repeated integrals) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 重積分法(MULTIPLE INTEGRATION) 目次 索引
3.7章で,区間 ![$[a,b]$](img158.png) で定義されている1変数関数の定積分をRiemann和を用いて定義しました.ここでは平面上の有界閉領域
で定義されている1変数関数の定積分をRiemann和を用いて定義しました.ここでは平面上の有界閉領域  で定義されている2変数関数の定積分を フランスの数学者 Jean Gaston Darboux(1842-1917) によって用いられた方法で定義します.
で定義されている2変数関数の定積分を フランスの数学者 Jean Gaston Darboux(1842-1917) によって用いられた方法で定義します.
長方形上の2重積分
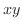 平面上の長方形
平面上の長方形 上で定義された関数を
上で定義された関数を
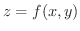 とします.次に
とします.次に  を
を  軸,
軸,  軸に平行な直線で分割し,分割された小長方形を
軸に平行な直線で分割し,分割された小長方形を
 とします.この分割を
とします.この分割を 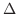 で表わします.つまり,
で表わします.つまり,



 は上に有界な集合で,
は上に有界な集合で,
 は下に有界な集合なので
は下に有界な集合なので

 が成り立ちます.ここで,特に
が成り立ちます.ここで,特に  が成り立つとき,
が成り立つとき, 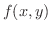 は
は  で積分可能であるといいます.また,この共通の値を,
で積分可能であるといいます.また,この共通の値を, 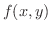 の 2重積分 といい,
の 2重積分 といい, 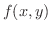 は
は  で2重積分可能(double integrable) であるといって,この値を次のように表わします.
で2重積分可能(double integrable) であるといって,この値を次のように表わします.

 の任意な点
の任意な点
 に対して,
に対して,


有界閉領域上の2重積分
次に,有界閉領域  上の積分を考えます.
上の積分を考えます.
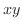 平面上の有界閉領域
平面上の有界閉領域  上で定義された関数を
上で定義された関数を
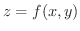 とします.図7.1 に示すように領域
とします.図7.1 に示すように領域  を内部に含む長方形を
を内部に含む長方形を  とし,
とし,  を
を  軸,
軸,  軸に平行な直線で分割し,分割された小領域(小長方形)を
軸に平行な直線で分割し,分割された小領域(小長方形)を
 とします.この分割を
とします.この分割を 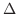 で表わします.ここで
で表わします.ここで  の内部に完全に含まれる小長方形の面積の和を
の内部に完全に含まれる小長方形の面積の和を
 ,
,  の点を含むすべての小長方形の和を
の点を含むすべての小長方形の和を
 とします.すると
とします.すると
 は上に有界な集合で,
は上に有界な集合で,
 は下に有界な集合です.これより,
は下に有界な集合です.これより,

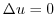 を
を  の 内面積(inner area),
の 内面積(inner area), 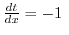 を
を  の 外面積(outer area) といいます.特に,
の 外面積(outer area) といいます.特に,  のとき,
のとき,  は 面積確定(mesurable area) であるといいます.そして,この共通の値を
は 面積確定(mesurable area) であるといいます.そして,この共通の値を  の面積といいます.
の面積といいます.
ここで,

 が
が  で積分可能であれば,
で積分可能であれば, 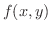 は
は  で積分可能であるといい,
で積分可能であるといい, 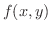 の
の  上の積分を次のように表わします.
上の積分を次のように表わします.

また,  の任意な点
の任意な点
 に対して,
に対して,

3変数関数 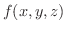 についても2変数の場合と同様に,3重積分が定義され,これを
についても2変数の場合と同様に,3重積分が定義され,これを

1変数のときと同じように,次の定理が成り立ちます.
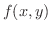 が面積確定である有界閉領域
が面積確定である有界閉領域  で連続ならば,
で連続ならば,  で
で 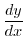 重積分可能である.
重積分可能である.
重積分の定義よりただちに次の公式が得られます.
 が面積確定な有界閉領域
が面積確定な有界閉領域  において連続であるとき,次の等式が成り立つ.
において連続であるとき,次の等式が成り立つ.
 が定数ならば,
が定数ならば,

 ならば
ならば


 平均値の定理
平均値の定理
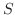 を領域
を領域  の面積とするとき
の面積とするとき

 が
が  内に存在する.
内に存在する.
証明
(1)  を
を  を含む長方形,
を含む長方形,  を
を  の面積とすると,
の面積とすると,
 |
 |
 |
|
 |
 |
||
 |
 |
