Next: Taylorの定理(Taylor's theorem) Up: 微分法(DIFFERENTIATION) Previous: 曲線の概形(curve sketching) 目次 索引
1章で極限値について学びましたが,
 のとき
のとき
 だとすると,
だとすると,

 と書くことにすると,同じように極限値が明白でない場合が,和,差,積,商,累乗などのときにも起こります.例えば,
と書くことにすると,同じように極限値が明白でない場合が,和,差,積,商,累乗などのときにも起こります.例えば,

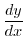 つの関数
つの関数 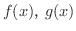 は閉区間
は閉区間 ![$[a,b]$](img158.png) で連続,開区間
で連続,開区間 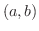 で微分可能とする.
で微分可能とする.
 で,しかも
で,しかも
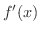 と
と
 が同時に 0 にならないならば,
が同時に 0 にならないならば,

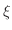 が少なくとも
が少なくとも 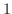 つ存在する.
つ存在する.
平均値の定理を 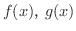 に適用すると,
に適用すると,



 と
と  の値は一般に等しくないので,この方法ではCauchyの平均値の定理は得
られません.
の値は一般に等しくないので,この方法ではCauchyの平均値の定理は得
られません.
証明 平均値の定理のときと同じように,Rolleの定理の条件を満たすような関数を考えます.

 となり,
となり, 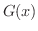 はRolleの定理の条件を満たす.したがって,Rolleの定理より,
はRolleの定理の条件を満たす.したがって,Rolleの定理より,

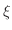 が少なくとも1つ存在する.ところで,
が少なくとも1つ存在する.ところで,

 ならば
ならば
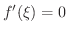 となり仮定に反する.したがって,
となり仮定に反する.したがって,
 となり,
となり,


極限値を求めるのに苦労した人もいると思いますが,次の定理はそんな人の味方です.この定理はフランスの数学者 G. F. A. L'Hospital (1661-1704) の名前をとってつけられました.最初に証明したのは彼の先生の Jakob Bernoulli (1654-1705)です.
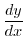 つの関数
つの関数 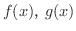 は閉区間
は閉区間 ![$[a,b]$](img158.png) で連続,開区間
で連続,開区間 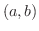 で微分可能とする.
で微分可能とする.
 で,しかも
で,しかも


証明
 である
である  をとると,Cauchyの平均値の定理より,
をとると,Cauchyの平均値の定理より,

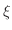 が少なくとも1つ存在する.したがって,
が少なくとも1つ存在する.したがって,

この定理は
 の場合も成り立ちます.
の場合も成り立ちます.
次の極限値を求めてみましょう.

解
これは
 の形の不定形です.そこで,分母,分子を別々に微分し,その商の極限値を求めると,
の形の不定形です.そこで,分母,分子を別々に微分し,その商の極限値を求めると,

 の形の不定形です.そこでもう一度,分母,分子を別々に微分し,その商の極限値を求めると,
の形の不定形です.そこでもう一度,分母,分子を別々に微分し,その商の極限値を求めると,

 の形の不定形です.そこでもう一度,分母,分子を別々に微分し,その商の極限値を求めると,
の形の不定形です.そこでもう一度,分母,分子を別々に微分し,その商の極限値を求めると,



さてL'Hospitalの定理は
 の不定形のときにしか使えないのでその他の不定形のときは,次のようにして
の不定形のときにしか使えないのでその他の不定形のときは,次のようにして
 の形に変形します.
の形に変形します.
(1)
 の場合,
の場合,

 を求めてみましょう.
を求めてみましょう.
解
これは
 の不定形をしています.そこで
の不定形をしています.そこで
 を
を
 と書き直すと
と書き直すと
 の不定形になり,L'Hospitalの定理より
の不定形になり,L'Hospitalの定理より

 より極限値は存在しません.
より極限値は存在しません.

不注意で
 にL'Hospitalの定理を用いると
にL'Hospitalの定理を用いると

 と書きたくなりますが,これは間違いです.
と書きたくなりますが,これは間違いです.
(2)
 の場合,
の場合,

 を求めてみましょう.
を求めてみましょう.
解
これは
 の不定形をしています.そこで
の不定形をしています.そこで
 を
を
 と書き直すと
と書き直すと
 の不定形になり,L'Hospitalの定理より
の不定形になり,L'Hospitalの定理より



(3)
 または
または
 の場合,
の場合,
 または
または
 を求めてみましょう.
を求めてみましょう.
解
これは
 の不定形をしています.そこで
の不定形をしています.そこで
 を
を
 と書き直すと
と書き直すと
 は
は
 の不定形なので
の不定形なので
 を
を
 と書き直すと,
と書き直すと,
 の不定形になり,L'Hospital の定理より
の不定形になり,L'Hospital の定理より
 |
 |
 |
|
 |
 |
