Next: ポインタと参照 Up: C++プログラミング入門 Previous: 関数 目次 索引
配列の概念(Concept of Arrays)
先に断っておくが,C++言語では,配列は次章で学ぶポインタとの間に強い関係があるので,配列はポインタと一緒に学ぶことを勧める.
プログラムを作るときには,データを変数という箱に入れて,これに変数名という名前を付けて扱った.しかし,この方法では,プログラムを作る上で非常に困難になることがある. 例えば,次のような例題である.
| 段数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 内容 | 微分学 | 積分学 | 線形代数 | C++言語 | 数値解析 | 応用数学 |
| 数量 | 95 | 100 | 55 | 80 | 60 | 40 |
ここで,キーボードから引き出しの段数を表す数を入力し,その内容物の数量を表示するプログラムを作成する.例えば,3と入力した場合には3段目の積分学の受講生の数55を表示し,4と入力した場合には4段目のC++言語の受講生の数80を表示するプログラムを作成せよ.
解答 1段目をdrawer1,2段目をdrawer2,とおくと, プログラムは
|
#include <iostream>
using namespace std; int main () { int drawer1 = 95; int drawer2 = 100; int drawer3 = 55; int drawer4 = 80; int drawer5 = 60; int drawer6 = 40; int i; cin >> i; if (i == 1) cout << drawer1; else if (i == 2) cout << drawer2; else if (i == 3) cout << drawer3; else if (i == 4) cout << drawer4; else if (i == 5) cout << drawer5; else cout << drawer6; } |
実行結果
![\begin{figure}% latex2html id marker 1884
\centering
\includegraphics[width=7.7cm]{CPPPIC/reidai6-1.eps}
\end{figure}](img151.png)
このプログラムでは,個々の場合を記述せねばならず,複雑で長くなる.もし,これが,大学全体の受講生となると,引出しの数が100や200では足りなくなってしまう.例えこれらの変数を個々に定義して表示できたとしても,長くて見通しの悪いプログラムになってしまうだろう.
そこで,このような場合に用いるものに,配列(array)というものがある.配列は「何番目のデータ」という表現ができる変数である.ベクトルや行列を配列を用いて表現することもできる.
|
1次元配列の宣言
[記憶クラス] データ型 配列名[要素数]; 2次元配列の宣言 [記憶クラス] データ型 配列名[行要素数][列要素数]; |
配列の初期化(Array Initialization)
|
1次元配列の宣言
[記憶クラス] データ型 配列名[要素数] = {初期値, ... , 初期値}; 2次元配列の宣言 [記憶クラス] データ型 配列名[行要素数][列要素数] = {{初期値, ... , 初期値}, ... , {初期値, ... , 初期値}}; |
| 要素数を省略すると,要素数は初期値の数となる. |
解答
1次元配列を用いるためには,変数を配列として定義する必要がある.例えば,
int drawer[6];
とすると,drawerという配列を用意し,そこには6個のデータが格納できることを意味する.このように配列の定義を行なうと,drawer[0],drawer[1],…,drawer[5]の合計6個の変数が用意される.ここで,drawer[0]と配列の要素番号は0から始まっていることに注意すること.また,
int drawer[] = {95,100,55,80,60,40};
とすると,配列drawer[]の初期化が行なわれる.
|
#include <iostream>
using namespace std; int main () { int i; int choice=0; int drawer[] = {95,100,55,80,60,40}; do { choice=1; cout << "数字を入力してください" << endl; cin >> i; if((i <=0) || (i > 6)) { cout << "1から6までの数字を入力してください" << endl; } else { cout << drawer[i-1] << endl; } cout << "続けたければ0を入力" << endl; cin >> choice; } while (choice==0); } |
実行結果
![\begin{figure}% latex2html id marker 1894
\centering\includegraphics[width=8.0cm]{CPPPIC/reidai6-2.eps}
\end{figure}](img152.png)
解答 配列名をaとすると,要素は浮動小数点型なので,float a[]またはdouble a[]と宣言する.初期化は,float a[7] = {22.2, 44.4, 66.6}とすると,残りの4つの要素には,自動的に0が挿入される.
|
#include <iostream>
using namespace std; int main() { float a[7] = {22.2, 44.4, 66.6}; int size = sizeof(a)/sizeof(float); for(int i=0;i < size;i++){ cout << "\ta[" << i << "] = " << a[i] << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 1904
\centering\includegraphics[width=8.0cm]{CPPPIC/reidai6-3.eps}
\end{figure}](img153.png)
2つの添え字をもつ配列を2次元配列という.例えば,
int data[3][2] = {1,2,3,4,5,6};
とすると,dataという配列を用意し,そこには3かける2,つまり6個のデータが格納できることを意味する.これは,data[0][0]=1; data[0][1]=2; data[1][0]=3; data[1][1]=4; data[2][0]=5; data[2][1]=6; と代入を行ったのと同じことである. また,括弧を用いて次のように書くこともできる.
int data[3][2] = {{1,2},{3,4},{5,6}};
配列を用いる基準
配列を学ぶと,配列の必要がないのに配列を用いたがる傾向が見られる.しかし,配列はメモリの消費,要素が同じ型だけなどの問題点があるので,配列を用いずにプログラムが組めるのであれば,配列は使わないようにする.
この時点で配列を用いるのは,データを蓄えておいて,後で再利用する場合や,そのデータの各要素をランダムに参照する場合などである. 後に,ベクタとよばれる配列よりももっと柔軟なオブジェクトについて学ぶ.
| 60 80 70 85 90 45 60 70 55 60 70 80 70 75 80 95 60 40 50 60 70 80 60 70 50 70 80 90 60 70 |
解答
これらのデータを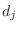 ,j=1,2,…30に格納する.平均mean,分散variance,標準偏差std_devは次の式で表せることに注意する.
,j=1,2,…30に格納する.平均mean,分散variance,標準偏差std_devは次の式で表せることに注意する.
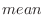 |
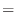 |
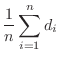 |
|
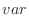 |
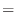 |
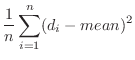 |
|
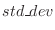 |
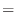 |
 |
この式に基づいて作成したプログラムは次のようになる.
まず,データを格納する配列をdata[30]とする.データを順に読み込むにはfor(i=0;i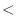 =29;i++)と配列は0から始まることに注意する.また,平方根を求めるためにsqrt()関数を用いるので,
=29;i++)と配列は0から始まることに注意する.また,平方根を求めるためにsqrt()関数を用いるので,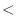 cmath
cmath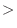 をインクルードしておく.
をインクルードしておく.
|
#include <iostream>
#include <cmath> using namespace std; int main () { int data[30]; double mean,variance,std_dev; int i,n = 30; double sum; for (i = 0;i < n; i++) { cout << i+1 << "番目のdata = " ; cin >> data[i]; } for (sum = 0.0,i = 0;i < n; i++) { sum = sum + data[i]; } double mean = sum/n; for( sum = 0.0,i = 0;i < n;i++) { sum = sum + (data[i] - mean)*(data[i] - mean); } double variance = sum/n; double std_dev = sqrt(variance); cout << "平均=" << mean << endl; cout << "分散=" << variance << endl; cout << "標準偏差 =" << std_dev << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1937
\centering\includegraphics[width=8.3cm]{CPPPIC/reidai6-4.eps}
\end{figure}](img161.png)
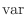 |
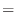 |
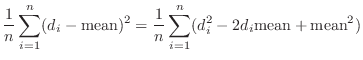 |
|
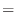 |
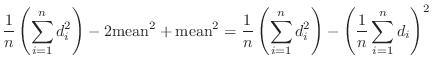 |
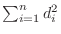 の計算も可能となる.
の計算も可能となる.
|
練習問題 6..1
標準偏差
1つのループで平均と平方和を求めるプログラムを作成せよ. |
2次元配列を用いた行列の計算(Matrix Calculation by 2dimensional Arrays)
2次元配列は,行列計算としての使い道が非常に多い.例えば,n行m列の行列は,次のように定義する.n=4,m=5とすると
float matrix[4][5];
または,マクロ名を用いて
|
#define ROW 4
#define COLUMN 5 float matrix[ROW][COLUMN]; |
| C++ではマクロ名を用いるのは薦められない. |
|
const int ROW = 4;
const int COLUMN = 5; float matrix[ROW][COLUMN]; |
配列では,確保する記憶量が多くなるが,2次元配列では,さらに多くの領域を必要とする.例えば,4行5列の2次元配列では20個の要素が必要で,ここでは要素の型がfloat形なので,20×4バイト →80バイトの領域が必要となる.double型にすると,20×8バイト → 160バイトの領域が必要になる.このこのことから,配列の型は,必要とする精度を考慮してなるべく確保する領域の小さい型を選ぶべきである.
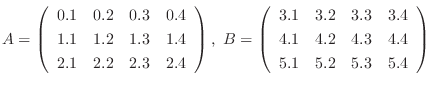
解答
行列A,Bは次のように定義できる.
float a[4][3], b[4][3];
または,constを用いて
const int ROW=3;
const int COLUMN=4;
とも定義できる.後々のことを考えるとconstを用いて定義しておくほうがよい.
まず,行列Aの成分を読み込む.行と列があるので,2重ループを作る.行ごとに読み込むには,外側のループが行で内側のループが列となる.つまり
for (i=0;i 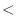 ROW; i++) {
ROW; i++) {
for (j=0;j  COLUMN;j++) {
COLUMN;j++) {
cout  "A["
"A["  i+1
i+1  "]["
"][" 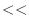 j+1
j+1 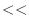 "]"
"]" 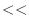 "=";
"=";
cin 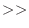 a[i][j];
a[i][j];
}
}
と書くと1行目に対して,1列目から4列目までを読み込むことになる.
準備はこのくらいにして,プログラムを作成しよう.
|
#include <iostream>
using namespace std; int main() { const int ROW=3; const int COLUMN=4; float a[ROW][COLUMN]; float b[ROW][COLUMN]; float c[ROW][COLUMN]; int i,j; for (i = 0;i < ROW; i++) { for (j = 0;j < COLUMN;j++) { cout << "A[" << i+1 << "][" << j+1 << "]" << "="; cin >> a[i][j]; } } for (i = 0;i < ROW; i++) { for (j = 0;j < COLUMN;j++) { cout << "B[" << i+1 << "][" << j+1 << "]" << "="; cin >> b[i][j]; } } for (i = 0;i < ROW; i++) { for (j = 0;j < COLUMN;j++) { c[i][j] = a[i][j] + b[i][j]; } } cout << "C:" << endl; for (i = 0;i < ROW; i++) { for (j = 0;j < COLUMN;j++) { cout << c[i][j] << " "; } cout << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 2026
\centering
\includegraphics[width=8.7cm]{CPPPIC/reidai6-5.eps}
\end{figure}](img167.png)
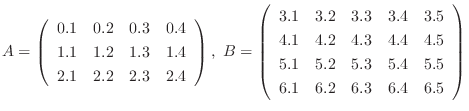
解答
行列の積は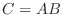 のとき,
のとき,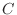 の
の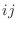 成分は
成分は
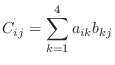
で求まることに注意する.これは和である.和の求め方は(s=s+f(j))であるので,
| C[i][j] = 0; |
| C[i][j] = C[i][j] + a[i][k] * b[k][j]; |
でC[i][j]が求まる.では,プログラムを作成しよう.
|
#include
<iostream>
using namespace std; int main() { const int ROW_A =3; const int COLUMN_A=4; const int ROW_B=4; const int COLUMN_B=5; float a[ROW_A][COLUMN_A]; float b[ROW_B][COLUMN_B]; float c[ROW_A][COLUMN_B]; int i,j,k; for (i = 0;i < ROW_A; i++){ for (j = 0;j < COLUMN_A;j++) { cout << "A[" << i+1 << "][" << j+1 << "]" << "="; cin >> a[i][j]; } } for (i = 0;i < ROW_B; i++) { for (j = 0;j < COLUMN_B;j++) { cout << "B[" << i+1 << "][" << j+1 << "]" << "="; cin >> b[i][j]; } } for (i = 0;i < ROW_A; i++) { for (j = 0;j < COLUMN_B;j++) { c[i][j] = 0; for (k=0;k < ROW_B;k++){ c[i][j] = c[i][j] + a[i][k] * b[k][j]; } } } cout << "C:" << endl; for (i = 0;i < ROW_A; i++) { for (j = 0;j < COLUMN_B;j++) { cout << c[i][j] << " "; } cout << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 2046
\centering
\includegraphics[width=7.9cm]{CPPPIC/reidai6-6.eps}
\end{figure}](img173.png)
1次元配列の関数への渡し方(Passing an Array)
配列のような多くのデータを関数に渡す場合,アドレス渡しまたは参照が用いられる.
解答1.アドレス渡し アドレス渡しでは,配列要素を1つ1つユーザ関数に渡すのではなく配列の先頭アドレスを渡し,関数側でポインタを用いて配列要素の参照を行なう. つまり,main関数の中で
|
と書き,関数ave_dataを float ave_data(float *x,int n) { float s=0; int i; for (i = 0;i < n;i++){ s = s + *x; x++; } return (s/n); } |
|
#include <iostream>
using namespace std; float ave_data(float * ,int ); int main() { const int MAX=10; int i,n; float ave, a[MAX]; cout << "データの個数を入力してください" << endl; cin >> n; for(i=0;i < n;i++){ cout << "a[" << i << "] ="; cin >> a[i]; } ave = ave_data(a,n); cout << "平均は=" << ave << endl; } float ave_data(float *x,int n) { float s=0; int i; for (i=0;i < n;i++){ s = s+*x; x++; } return s/n; } |
![\begin{figure}% latex2html id marker 2058
\centering
\includegraphics[width=8.2cm]{CPPPIC/reidai6-7.eps}
\end{figure}](img174.png)
解答2.参照渡し main関数で配列aにデータを入力し,そのデータを平均値を求める関数ave_data()に渡す.そのためには,仮引数をfloat x[]と書けばよい.float x[]により,配列名がxでその要素は実数型であることがコンパイラーに伝えられる.また,xは配列のアドレスを格納しているので,コンパイラが配列を宣言するための情報は全て満たされている.ただし,C++では,配列の要素数も一緒に渡す必要がある.つまり,main関数の中で
|
と書き,関数ave_dataを float ave_data(float x[ ],int n) { float s=0; for (int i = 0;i < n;i++){ s = s + x[i]; } return (s/n); } |
とすれば,main関数の中でave_data(a,n)が呼ばれたとき,配列aの先頭アドレスが関数に渡される.なぜなら,aの値は配列の先頭アドレスである.関数はそのアドレスを使って,配列の要素の変更を行なう.配列の関数への受け渡しは,変数のアドレス渡しと同じようである.その後,関数ave_data()は平均を計算し,その値をmain関数に戻す.では,プログラムを作成しよう.
|
#include <iostream>
using namespace std; float ave_data(float * ,int ); int main() { const int MAX=10; int i,n; float ave, a[MAX]; cout << "データの個数を入力してください" << endl; cin >> n; for(i=0;i < n;i++){ cout << "a[" << i << "] ="; cin >> a[i]; } ave = ave_data(a,n); cout << "平均は=" << ave << endl; } float ave_data(float x[],int n) { float s=0; for (int i=0;i < n;i++){ s = s+x[i]; } return s/n; } |
![\begin{figure}% latex2html id marker 2063
\centering
\includegraphics[width=8.2cm]{CPPPIC/reidai6-7.eps}
\end{figure}](img175.png)
|
練習問題 6..2
データの最小値
最小値を返す関数float min(float a[], int n)を作成し,テストせよ.ただし,次の5個のデータを読み込むとする.10.23, 12,32, 11.24, 13.11, 10.01. |
線形探索法(Linear Search algorithm)
データは多くの場合配列を用いて格納されている.この配列の中から,求めているものを探し出す最も単純な方法は,順に調べていく方法だろう.この方法を線形探索法という.例えば,22, 44, 66, 88, 44, 66, 55の中から88を先頭から1つずつ順に調べて見つかれば終了という方法である.
解答
配列aをint a[] = {22, 44, 66, 88, 44, 66, 55}とし,探索している数と等しい要素があったら,そのときの位置を返し,等しい要素がなかったら要素の数を返す.
配列は0番から始まっていることに注意し,
i=0からi 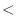 nの間
nの間
(a[i] == x)ならば,iを返し, そうでなければ,nを返す関数を
int index (int x, int a[], int n)
とする.
|
#include <iostream>
using namespace std; int index(int,int[],int); int main() { int a[] = {22, 44, 66, 88, 44, 66, 55}; cout << "index(44,a,7) = " << index(44,a,7) << endl; cout << "index (50,a,7) = " << index(50,a,7) << endl; } int index(int x, int a[], int n) { for (int i=0; i < n ; i++) { if (a[i] == x) { return i; break; } } return n; } |
実行結果
![\begin{figure}% latex2html id marker 2087
\centering
\includegraphics[width=8.2cm]{CPPPIC/reidai6-8.eps}
\end{figure}](img176.png)
return i;の後にbreak;でループから脱出している.このことにより,無駄な計算を省略することができる.C++言語のようにループから強制脱出するスマートな制御構造をもつ場合は番兵を使わないでプログラムが書けるので,わざわざ余分なデータを入れて番兵を立てる必要はない.
|
練習問題 6..3
得点の順位付け
得点が22, 44, 66, 88, 44, 66, 55, 78, 80, 48と与えられているとき,55点の順位を調べるプログラムを作成せよ. 55点の順位を表す変数rankの初期値を1とし,データの先頭から終わりまで順に55点と比較し,55点を越えるものがあれば,rankを+1する. |
基本交換法(バブルソート)(Bubble Sort Algorithm)
線形探索法はあまり効率の良いアルゴリズムではない.電話帳で名前を探すときには,絶対に使わない方法だろう.電話帳で名前を探すときには,50音順でまず調べ,そこから目的の名前を探すことになる.このように既に名前の順(昇順)になっていれば,探す効率が良くなる.これは,配列から必要なものを探すときも同様である.配列の要素が順に並んでいれば,もっと簡単に探索ができる.そこで,まず配列の要素を順に並べることを考える.配列の要素を順に並べることを整列またはソート(sort)という.
データの整列には,いろいろなアルゴリズムが開発されている.他のアルゴリズムに比べると効率は良くないが,考え方が最も分かりやすい基本交換法(バブルソート)を紹介する.
バブルソートによるデータの整列は,配列の前(または後)から順に隣り合う要素同士を比較し,大小関係に逆転がある場合にはデータの交換を行なうという走査の繰り返しによってなされる.次のデータを昇順に並べることを考える.35, 50, 10, 99, 43.
下の表に示すように,最初の走査によって最も値の大きな要素がH(5)に入る.したがって,2回目の走査はH(1)からH(4)まででよいことがわかる.このように,範囲を縮小しながら走査をN-1回繰り返すと求める結果が得られる.これより,最悪の場合は,N + N-1 + 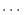 + 1 =
+ 1 =
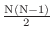 回の入れ替えを行なわなければならないことが分かる.
回の入れ替えを行なわなければならないことが分かる.
| H(1) | H(2) | H(3) | H(4) | H(5) | 交換 | |
| 35 | 50 | 10 | 99 | 43 |  |
しない |
| 35 | 50 | 10 | 43 | 99 |  |
する |
| 35 | 10 | 50 | 43 | 99 |  |
する |
| 35 | 10 | 43 | 50 | 99 |  |
しない |
| 35 | 10 | 43 | 50 | 99 |  |
する |
| 10 | 35 | 43 | 50 | 99 |  |
しない |
| 10 | 35 | 43 | 50 | 99 |  |
しない |
| 10 | 35 | 43 | 50 | 99 |
解答 double a[] = {55.4, 22.1, 66.5, 44.3, 99.8, 88.7, 77.6, 33.2};とし,a[i]とa[i+1]を比較し,a[i] 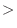 a[i+1]ならば,swap()関数を用いて入れ替える.swap()関数は標準C++汎用アルゴリズムで
a[i+1]ならば,swap()関数を用いて入れ替える.swap()関数は標準C++汎用アルゴリズムで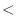 algorithm
algorithm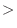 で定義されている.
で定義されている.
|
#include <iostream>
#include <algorithm> using namespace std; void print(double[],int); void sort(double[],int); int main() { double a[] = {55.4, 22.1, 66.5, 44.3, 99.8, 88.7, 77.6, 33.2}; print(a,8); sort(a,8); print(a,8); } void sort(double a[], int n) { // バブルソート for (int i=1; i < n; i++){ for(int j=0;j < n-i;j++){ if(a[j] > a[j+1]) { swap(a[j],a[j+1]); } } } } void print(double a[], int n) { for (int i=0;i < n;i++){ cout << " "; } cout << endl; } |
実行結果
![\begin{figure}% latex2html id marker 2136
\centering
\includegraphics[width=9.7cm]{CPPPIC/reidai6-9.eps}
\end{figure}](img179.png)
この他にも整列のアルゴリズムの基本形として,基本選択法(選択ソート) ,基本挿入法(挿入ソート)がある.また,整列のアルゴリズムの基本形の改良形として,改良交換法(クィックソート),改良選択法(ヒープソート),改良挿入法(シェルソート)がある.さらに,2つのデータを併合する方法としてマージソートがある.この中の基本選択法(選択ソート) ,基本挿入法(挿入ソート)については,演習問題で取り上げる.
|
練習問題 6..4
バブルソート
次のデータを降順に並べるプログラムを作成せよ.
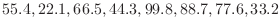
|
2分探索法(Binary Search Algorithm)
線形探索法は効率が悪いと言う話をしたが,線形探索法で,n個のデータの中にあるデータが含まれているかを探索すると,最悪の場合全てのデータをチェックしなければならない.つまり,n回のチェックが必要である.次に紹介する方法は,最悪の場合でも
![${\rm [\log_{2}{n}]+1}$](img180.png) 回のチェックで探索ができる方法で,2分探索法とよばれる方法である.2分探索法を用いるための前提条件は,データが整列されていることである.
回のチェックで探索ができる方法で,2分探索法とよばれる方法である.2分探索法を用いるための前提条件は,データが整列されていることである.
2分探索法はn個の要素が昇順に並んでいる配列を中点で2つの部分に分けて,求めようとしている値が入っている方を新たな配列とし,同じことを繰り返す方法である.例えば,6個の要素a[0]からa[5]を持つ配列aがあるとする.このとき,2分探索法を用いると0と5の中点として,整数の割り算より(0+5)/2=2が求まる.そこで,a[2]と探しているxが等しければ,探索は終了.等しくなければ,a[2] 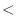 xまたはa[2]
xまたはa[2] 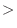 xのどちらかである.そこで,求めるxはa[0]からa[1]の間かa[3]からa[5]の間である.こうやって,区間を半分にしていくので,n個の要素を持つ配列でも,
xのどちらかである.そこで,求めるxはa[0]からa[1]の間かa[3]からa[5]の間である.こうやって,区間を半分にしていくので,n個の要素を持つ配列でも,
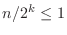 になれば探索は終了する.したがって,
になれば探索は終了する.したがって,
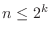 より,
より,
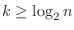 となる.この式を満たす最小の
となる.この式を満たす最小の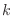 は
は
![${\rm [\log_{2}{n}]+1}$](img180.png) となる.例えば,
となる.例えば,
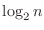 が3.5のときを考えると,
が3.5のときを考えると,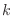 は整数より,4となることから分かるだろう.
は整数より,4となることから分かるだろう.
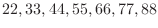
解答
|
#include <iostream>
using namespace std; int index(int,int[],int); int main() { int a[] = {22, 33, 44, 55, 66, 77, 88}; cout << "index(44,a,7) = " << index(44,a,7) << endl; cout << "index(60,a,7) = " << index(60,a,7) << endl; } int index(int x, int a[], int n) { //2分探索法 int lo = 0, hi = n-1, i; while(lo < hi){ i = (lo + hi)/2; if(a[i] == x) { return i; break; } if(a[i] < x){ lo = i+1; } else { hi = i-1; } } return n; } |
実行結果
![\begin{figure}% latex2html id marker 2168
\centering
\includegraphics[width=9.7cm]{CPPPIC/reidai6-10.eps}
\end{figure}](img187.png)
型定義(Type Definitions)
列挙型はプログラマ自身が自分で型を定義する方法の1つである.例えば,
enum Color {RED, ORANGE, YELLOW, GREEN, BLUE, VIOLET};
はColor型を定義し,次のように用いることができる.
|
Color shirt = BLUE;
Color wavelength[VIOLET+1] = {420,480,530,570,600,620}; |
ここで,変数shirtは型Colorの中の6個の値のどの値でもとることができ,ここでは,BLUEの値で初期化されている.
C++には,この他にも標準型の名前を変更する方法を用意している.予約語typedefにより指定された型に新しい名前(シノニム,エイリアス)を宣言することができる.その構文は
| typedef 型 エイリアス;
|
typedef宣言は新しい型を提供するのではなく,すでにある型のシノニム(同義語)を提供するだけである.
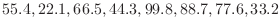
解答
|
#include <iostream>
#include <algorithm> using namespace std; typedef float Sequence[]; void print(Sequence,int); void sort(Sequence,int); int main() { Sequence a = {55.4, 22.1, 66.5, 44.3, 99.8, 88.7, 77.6, 33.2}; print(a,8); sort(a,8); print(a,8); } void sort(Sequence a, int n)
{ // バブルソート
|
実行結果
![\begin{figure}% latex2html id marker 2185
\centering
\includegraphics[width=9.7cm]{CPPPIC/reidai6-11.eps}
\end{figure}](img188.png)
1. 配列の要素は何通りの型を同時に持つことができるか.
2. 配列の添え字の型とその範囲がとる値について述べよ.
3. 配列の大きさより初期化の値が少ないとき,配列の要素はどんな値をとるか述べよ.
4. 列挙型enum文とtypedef文の違いについて述べよ.
1. 基本選択法(Selection Sort)の関数のプログラムコードを書きなさい. 基本選択法は,n個のデータの中から最大なものa[j]を探し,それと末尾の項a[n-1]と交換する.次に,残りのn-1個のデータから最大なものを探し,それと末尾の項a[n-1]と交換する.この操作を繰り返す方法である.
2. 基本挿入法(Insertion Sort)の関数のプログラムコードを書きなさい.基本挿入法は,a[0]~a[n-1]のa[0]~a[i-1]がすでに整列されているとして,a[i]がどこに入るか調べて,適当な位置に挿入する方法である.
例えば,数列3,4,1,5,2を整列するとし,四角で囲まれた数字を挿入した数字とすると,
| 3 |
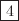 |
|||
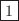 |
3 | 4 | ||
| 1 | 3 | 4 |
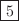 |
|
| 1 |
 |
3 | 4 | 5 |