Next: 関数 Up: C++プログラミング入門 Previous: 選択(selection) 目次 索引
反復(Loop)
ループとは繰り返し文のことである.俗に反復処理(iteration)と呼ばれていて構造化プログラミングの根幹をなしている.反復処理にはwhile文,do-while文とfor文がある.
その昔,コンピュータの性能が悪かった時代,また,しっかりした制御構造および反復処理がプログラミング言語に用意されたいなっかた時代,多くの人がgoto文と呼ばれるジャンプを使ってプログラムを書いていた.しかし,1960年代後半goto文によって書かれたプログラムは,他人にとってわけのわからないプログラム(スパゲッティプログラム)になり,諸悪の根源であると言われ始めた.このことより,ソフトウェアも通常の工業製品と同じように生産管理が必要であるという観点から「ソフトウェア工学」が生まれた.このような流れの中から,分かりやすいプログラムを書くための方法論がダイクストラによって提案され,その中の1つに「構造化プログラミング」がある.
構造化プログラミング(Structured Programming)
構造化プログラミングは,基本的に3つの構造から成り立っている.
|
連接(sequence):プログラムは上から下に流れる
選択構造(Selection) 反復処理(Iteration) |
構造化定理によると,すべてのアルゴリズムはこの3つの構造だけで記述できることが証明されている.
現在,C++言語を学んでいる学生は,上記の1,2,3だけでアルゴリズムを書く練習をして欲しい.なお,今やプロジェクトの規模が大きくなり,構造化プログラミングを用いても,ある時点からは複雑さがプログラマの管理できる限界を超えてしまっている.そこで生まれたのが,オブジェクト指向という考え方である.C++言語はオブジェクト指向言語としての顔も持つ.このテキストで,徐々にオブジェクト指向言語としてのC++についても学んで行く.
while文(while Statement):~の間~する
|
while文の構文は
while(条件式){ 式文; } |
の形をとる.while文は条件式が成立しなければ0を返し,次の式文は実行されないでwhile文の次に続く文に飛ぶ.条件式が成立すると0以外を返し,式文が条件が0になるまで実行される.したがって,while文は式文を一つも実行せず,while文を終えることもある.
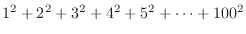 を求めるプログラムをwhileループを用いて作成せよ.
を求めるプログラムをwhileループを用いて作成せよ.
解答 求める和をsとおくと,
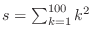 と表せる.
と表せる.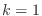 のとき,
のとき,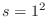 .
. 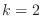 のとき,
のとき,
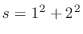 となるが,
となるが,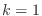 のとき,
のとき,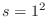 としておくと,
としておくと,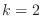 のとき,
のとき,
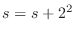 と表せることに気づいただろうか.これが数列の和のコーディングの方法である.
と表せることに気づいただろうか.これが数列の和のコーディングの方法である.
この問題では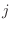 番目が
番目が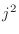 より和は
より和は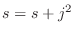 と表せる.これを
と表せる.これを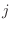 が1から100まで行えばよいので,擬似コードで書くと,
が1から100まで行えばよいので,擬似コードで書くと,
j
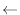 1, s
1, s
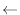 0;
0;
while (j 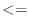 100) do
100) do
s
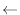 s +
s + 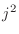 ;
;
j
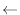 j+1;
j+1;
となる.これをC++言語に書き直すと,
|
#include <iostream>
using namespace std; int main() { int j=1,s=0; while(j <=100){ s = s + j*j; j+=1; } cout << s << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1168
\centering
\includegraphics[width=8.3cm]{CPPPIC/reidai4-1.eps}
\end{figure}](img74.png)
一般に,j番目がある関数f(j)で表せるならば,上の式文s = s + j*j;をs=s+f(j)と書き換えればよい.
|
練習問題 4..1
数列の和
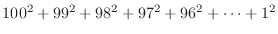 をこの順で求めるプログラムをwhileループを用いて作成せよ. をこの順で求めるプログラムをwhileループを用いて作成せよ. |
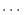 1/nを求めるプログラムを作成せよ.ただし,nは逆数の和sが入力された整数より大きくなる最初の整数とする.
1/nを求めるプログラムを作成せよ.ただし,nは逆数の和sが入力された整数より大きくなる最初の整数とする.
解答 逆数の和をsumとし,入力された値をboundとすると,
i
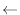 0;
0;
while(sum 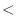 bound) do
bound) do
sum
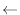 sum + 1.0/++i;
sum + 1.0/++i;
で逆数の和が入力された値より大きくなる最初の整数iを求めることができる.C++言語に書き直すと,
|
#include <iostream>
using namespace std; int main() { int bound; cout << "正の整数を入力して下さい: " ; cin >> bound; double sum = 0.0; int i = 0; while(sum < bound){ sum += 1.0/++i; } cout << "最初の" << i << "項の逆数の和は" << sum << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1190
\centering
\includegraphics[width=8.0cm]{CPPPIC/reidai4-2.eps}
\end{figure}](img77.png)
|
練習問題 4..2
逆数の和
sum = 1 + 1/2 + 1/3 + 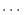 + 1/1000とrsum = 1/1000 + 1/999 + + 1/1000とrsum = 1/1000 + 1/999 + 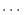 + 1をfloatで宣言し求めるプログラムを作成せよ.sumとrsumの値を比較せよ.また,どちらが正確か考えよ.さらに,このとき発生した誤差はなんと言われるか. + 1をfloatで宣言し求めるプログラムを作成せよ.sumとrsumの値を比較せよ.また,どちらが正確か考えよ.さらに,このとき発生した誤差はなんと言われるか. |
解答 素因数とは,与えられた和nの約数でかつ素数のことである.素数とは,それ自身と1でしか割れない数である.ただし,1は素数には入れない.例えば,nを120とすると,nの約数は,2,3,5であり,120の素因数分解を行なうと,
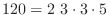 となる.
となる.
| 2 | 120 |
| 2 | 60 |
| 2 | 30 |
| 3 | 15 |
| 5 |
では,素因数分解をおこなうアルゴリズムを考えてみる.データnを読み取って,2から順に割っていき,ある数mで割れたら商n/mを新たなnとおき,さらにmで割り切れなくなるまで続ける.mで割り切れなくなったらmを1増加し,nを割っていくことを繰り返し,商nが1になるまで続ける.このとき発生した,mが素因数となる.表示するときに,最後の数字のあとには「,」を付けないようにする. では,プログラムを作成しよう.
|
#include <iostream>
using namespace std; int main () { int m=2,n; char c = ' '; cout << "整数を入力してください."; cin >> n; while(n!= 1){ while(n%m == 0){ n = n/m; cout << c << m; c = ','; } m++; } } |
実行結果
![\begin{figure}% latex2html id marker 1215
\centering
\includegraphics[width=7.9cm]{CPPPIC/reidai4-3.eps}
\end{figure}](img79.png)
最後の約数の後にはカンマをつけないようにするには,カンマを約数の前に出力させる.そこで,問題になる最初のカンマを空白文字にしておけばよい.
解答
素数とは1とその数自身でしか割ることができない数である.そこで,与えられた数をnumとし,numを2から順にnum-1までの数で割っていき,割り切れなければ素数であることが示せる.numを割る数をdivisorとし,divisorが2から順に割っていくということをプログラムで書くと,divisorがnより小さい間は実行すると表せるのでwhile(divisor 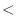 num)と書ける.次に,whileループを実行中あまり(remainder)の最小値(min_remainder)を求める.やがて,divisorがnumに到達しwhileループが終了する.その後,あまりの最小値(min_remainder)の値が0か0以外かを調べれば,numが素数かどうかの判定ができる.プログラムに書くと次のようになる.
num)と書ける.次に,whileループを実行中あまり(remainder)の最小値(min_remainder)を求める.やがて,divisorがnumに到達しwhileループが終了する.その後,あまりの最小値(min_remainder)の値が0か0以外かを調べれば,numが素数かどうかの判定ができる.プログラムに書くと次のようになる.
|
#include <iostream>
using namespace std; int main () { int num,min_remainder=1,remainder,divisor=2; cout << "整数を入力してください" << endl; cin >> num; if(num == 1){ min_remainder=0; } while(index < num){ remainder = num%divisor; if(remainder < min_remainder){ min_remainder=0; } divisor++; } if(min_remainder !=0){ cout << num << "は素数です" << endl; } else{ cout << num << "は素数ではありません" << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 1225
\centering
\includegraphics[width=8.0cm]{CPPPIC/reidai4-4.eps}
\end{figure}](img80.png)
もう少しよく考える.2で割り切れる数(偶数)は2以外素数ではない.また,素数でない数(合成数)の約数は対になっているので,nの平方根までの数をチェックすればよいことが分かる.この考えを用いて,もう一度プログラムを作成しよう.
|
//素数判定改良版
#include <iostream> using namespace std; int main () { int num,min_remainder=1; cout << "整数を入力してください" << endl; cin >> num; if(num == 1 || num > 2 && num%2 == 0){ min_remainder=0; } int divisor = 2; while(divisor*divisor < num){ int remainder = num%divisor; if(remainder < min_remainder){ min_remainder=0; } index++; } if(min_remainder !=0){ cout << num << "は素数です" << endl; } else{ cout << num << "は素数ではありません" << endl; } } |
ループによる実行回数のコントロール(Control of Execution by Loop)
こういうプログラムを実行させるとき,その都度エグゼファイル(実行ファイル)を立ち上げなければならず,面倒であると感じた人は少なくないだろう.そこで,好きなだけ実行し,止めたくなったら止めることができる方法を考えてみる.
whileループは条件式が満たされている間,whileブロックを実行する.そこで,例えば条件式を,入力されたデータが正の値の間は正しいとすれば,入力データが負になるまでは実行することができる.例えば,
|
int choice=0;
while (choice >= 0) { cout << "続ける場合は正の数字をやめるときは負の数字を入力してください"; cin >> choice; } |
ループからの脱出(Terminating a Loop)
while,for,do-while文を用いるとき,気をつけなければならないのは,無限ループにおちいりやすいことである.このようなことを避けるために,ループの条件は点ではなく,区間とするべきである.特に,while(1),for(;;)などの無限ループではじめ,Ctrl+Cで脱出するようなプログラムは初心者は可能なかぎり書くべきではない.
さて,ループからどうしても脱出する必要があるときには,if文とbreak文を用いる.例えば,キーボードからデータを入力して,0を入力したら終了したい場合を考えよう.入力されたデータを変数dataに取り込むとすると,データがある限り読み込むとすると,
whileループの条件はcin 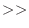 dataと書ける.ここで,cinは呼び込みに成功すると1を返し,失敗すると0を返すので,このループは入力がある限り続行される.次に,入力が0のとき,if文の条件が真となるので,次のbreak文に到達し,ここで,whileループから脱出する.
dataと書ける.ここで,cinは呼び込みに成功すると1を返し,失敗すると0を返すので,このループは入力がある限り続行される.次に,入力が0のとき,if文の条件が真となるので,次のbreak文に到達し,ここで,whileループから脱出する.
|
while(cin >> data)
{ if (data == 0){ break; } } |
ループから脱出するもう一つの方法は,breakの代わりに関数exit (0)を用いる方法である.この方法はループから脱出するばかりでなく,プログラムを終了してしまう.
|
練習問題 4..3 次の条件を満たす正の整数を小さい方から3個見つけるプログラムを作成せよ.
正の整数nは3で割ると1余り,5で割ると2余り,7で割ると3あまる数である.つまり,n%3 == 1, n%5 == 2, n%7 == 3を同時に満たす数である. |
解答
int max,min,ini;
cin 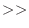 ini;
ini;
max = min = ini;
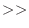 data){
data){
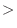 max) {
max) {
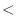 min) {
min) {
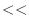 "平均は"
"平均は" 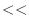 sum/n
sum/n 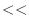 endl;
endl;
以上をまとめると次のようなプログラムになる.
|
#include <iostream>
using namespace std; int main () { int data,ini; cout << "数学の成績を入力してください." << endl; cin >> ini; double sum = ini; int max = min = ini; int n = 1;
while(cin >> data){
|
実行結果
![\begin{figure}% latex2html id marker 1263
\centering
\includegraphics[width=8.0cm]{CPPPIC/reidai4-5.eps}
\end{figure}](img81.png)
|
練習問題 4..4
平均,最大・最小値
データをキーボードから入力し,入力したデータの平均を求めるプログラムを作成せよ.ただし,負の値を入力した時点で終了するとする. |
do ... while文(do ... while Statement)
|
do ... while文の構文は
do { 式文; }while(条件式); |
| 最低一回は必ず実行される. |
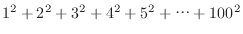 を求めるプログラムをdo...whileループを用いて作成せよ.
を求めるプログラムをdo...whileループを用いて作成せよ.解答
==============================================
#include 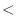 iostream
iostream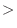
using namespace std;
int main()
{
int j=1,s=0;
do {
s = s + j*j;
j+=1;
} while(j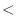 =100);
=100);
cout 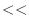 s
s 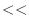 endl;
endl;
}
==============================================
実行結果
![\begin{figure}% latex2html id marker 1290
\centering
\includegraphics[width=8.0cm]{CPPPIC/reidai4-6.eps}
\end{figure}](img83.png)
|
練習問題 4..5
数列の和
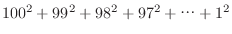 を求めるプログラムをdo...whileループを用いて作成せよ.1190 を求めるプログラムをdo...whileループを用いて作成せよ.1190 |
階乗0!,1!,2!,3!,...は次の漸化式により定義されている.
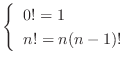
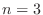 のとき,
のとき,
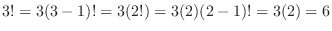
解答 階乗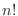 を
を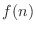 とすると,
とすると,
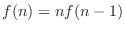 で与えられる.そこで,
で与えられる.そこで,
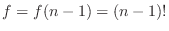 とおくと,階乗を求める構文は,繰り返しを用いて
とおくと,階乗を求める構文は,繰り返しを用いて
f = f * n
となる.この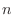 を1から順に増やしていけば,全ての階乗を求めることができる.よって,擬似コードで書くと
を1から順に増やしていけば,全ての階乗を求めることができる.よって,擬似コードで書くと
入力 bound;
i
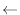 1;
1;
f
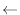 1;
1;
do
f
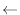 f
f 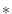 (++i);
(++i);
while(i 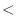 入力);
入力);
となる.例題5.11では再帰(recursion)を用いてn!を求めている.
|
#include <iostream>
using namespace std; int main() { long bound; cout << "正の整数を入力して下さい: "; cin >> bound; cout << bound << "までの階乗は \n 1"; long f= 1, i = 1; do { f *= ++i; cout << ", " << f; }while(f < bound); } |
実行結果
![\begin{figure}% latex2html id marker 1318
\centering
\includegraphics[width=11.7cm]{CPPPIC/reidai4-7.eps}
\end{figure}](img93.png)
for文(for Statement)
|
for文の構文は
for (初期値;条件式;更新){ 式文; } |
の形をとる.
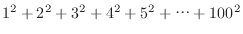 を求めるプログラムをforループを用いて作成せよ.
を求めるプログラムをforループを用いて作成せよ.解答
|
#include <iostream>
using namespace std; int main() { int s=0; for(int j=1; j<=100;j++){ s = s + j*j; } cout << s << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1355
\centering
\includegraphics[width=8.5cm]{CPPPIC/reidai4-8.eps}
\end{figure}](img96.png)
|
練習問題 4..7
forループを用いた数列の和
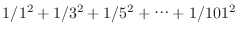 を求めるプログラムをforループを用いて作成せよ.1201 を求めるプログラムをforループを用いて作成せよ.1201 |
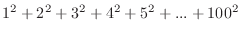 を
を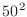 までとそれ以降に分けて求めるプログラムをforループを用いて作成せよ.
までとそれ以降に分けて求めるプログラムをforループを用いて作成せよ.解答
|
#include <iostream>
using namespace std; int main() { int s=0; for(int j=1; j<50;j++){ s = s + j*j; } for(int j=50; j<=100;j++){ s = s + j*j; } cout << s << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1375
\centering
\includegraphics[width=8.6cm]{CPPPIC/reidai4-9.eps}
\end{figure}](img100.png)
この例題ではコントロール変数iが2つのforループで用いられている.ANSIのC++以前のコンパイラではエラーになる.
実行結果
![\begin{figure}% latex2html id marker 1384
\centering
\includegraphics[width=11.7cm]{CPPPIC/reidai4-10.eps}
\end{figure}](img101.png)
解答
|
#include <iostream>
using namespace std; int main() { long bound; cout << "正の整数を入力して下さい: "; cin >> bound; cout << bound << "までの階乗は \n 1"; long f= 1; for(int i=2; f < bound; i++) { f *= i; cout << ", " << f; }while(f < bound); } |
forループはなかなかしなやかで,ステップ幅が1より大きいforループも可能である.
解答 4以下の整数で1以外は素数です.5以上の素数は全て奇数.そこで,まず,偶数か調べ,偶数なら素数でないことが分かる.次に,奇数で割って余りが0になれば素数ではない.
|
#include <iostream>
using namespace std; int main() { int n; cout << "整数を入力してください" << endl; cin >> n; if(n < 2){ cout << n << "は素数ではありません" << endl; } else if(n < 4) { cout <<< n << "は素数です" << endl; } else if(n%2 == 0){ cout << n << " = 2*" << n/2 << endl; } else { for(int d=3; d < n/2; d+=2){ if(n%d == 0) { cout << n << " = " << d << "*" << n/d << endl; exit(0); } } cout << n << "は素数です" << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 1395
\centering
\includegraphics[width=11.7cm]{CPPPIC/reidai4-11.eps}
\end{figure}](img102.png)
実行結果
![\begin{figure}% latex2html id marker 1404
\centering
\includegraphics[width=3.3c...
...dai4-12.eps}
\includegraphics[width=3.4cm]{CPPPIC/reidai4-12-1.eps}
\end{figure}](img103.png)
解答
<実行結果1>
cout 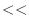 "*";
"*";
で1つのアスタリスクを表示することができる.では*****と表示するにはどうすればよいだろうか.確かにcout 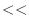 "*****";でもできるが,これではアスタリスクを任意の数だけ表示せよとなると,不可能である.そこで,cout
"*****";でもできるが,これではアスタリスクを任意の数だけ表示せよとなると,不可能である.そこで,cout 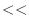 "*";を5回実行すると*****が表示できることに気づけばよい.5回実行させるには,例えばforループを用いるとfor(i=1;i
"*";を5回実行すると*****が表示できることに気づけばよい.5回実行させるには,例えばforループを用いるとfor(i=1;i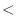 =5;i++)と書けばよいことを知っている.次に,第1回目には,1つのアスタリスク,第2回目は2つのアスタリスクと増やすにはどうすればよいだろうか.i
=5;i++)と書けばよいことを知っている.次に,第1回目には,1つのアスタリスク,第2回目は2つのアスタリスクと増やすにはどうすればよいだろうか.i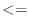 5の5の代わりに,jを用いて,
5の5の代わりに,jを用いて,
for(int j=1;j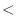 =5;j++){
=5;j++){
for(int i=1;i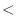 =j;i++){
=j;i++){
cout 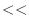 "*";
"*";
}
}
と書けば,外側のループが1回終了する間に内側のループがj回実行されることになる.内側のループが終了したら,endl;で改行する.ではプログラムを作成しよう.
|
#include <iostream>
using namespace std; int main() { for(int j=1; j <= 5; j++){ for(int i=1; i <= j; i++){ cout << "*"; } cout << endl; } } |
<実行結果2>
実行結果1との違いはアスタリスクを右詰めで表示しているところである.そこで,アスタリスクの前にブランクを挿入するコマンドを追加すればよい.
|
#include <iostream>
using namespace std;
int main() { int k; for(k = 4; k >= 0; k$--$){ for(int j=1; j <= k; j++){ cout << " "; } for(int i=1; i <= 5-k; i++){ cout << "*"; } cout << endl; } } |
|
練習問題 4..8
反復練習
次のような形を表示するプログラムを作成せよ. |
![\begin{figure}% latex2html id marker 1433
\centering
\includegraphics[width=3.0cm]{CPPPIC/renshu4-7.eps}
\end{figure}](img104.png)
continue文(continue Statement)
break文はループブロックのbreak文以下をスキップし,ループの外の次の文にジャンプする.continue文もbreak文のように,ループブロックをスキップするが,ループを終了する代わりに,ループの次の反復にうつる.
|
#include <iostream>
using namespace std; int main() { int n; for(; ;){ cout << "整数を入力して下さい:"; cin >> n; if(n%2 == 0) continue; if(n%3 == 0) break; cout << "\tループの最後" << endl; } cout << "\tループの外" << endl; } |
解答 2でも3でも割り切れない数を入力すると,2つのif文の条件を満たさないので,ループの最後が出力される.2で割り切れる数を入力すると,continueで残りの式文をスキップし,ループに戻る.3で割り切れる数を入力すると,break文でループの外に出る.,
実行結果
![\begin{figure}% latex2html id marker 1443
\centering
\includegraphics[width=8.0cm]{CPPPIC/reidai4-13.eps}
\end{figure}](img105.png)
擬似乱数(Pseudo-Random Number)
コンピュータの応用で最も重要なものの1つに現実世界のシミュレーションがある.ハイテクリサーチや開発の多くがシミュレーションを用いて,どのようにシステムが動いているかを実際に実験を行わずに研究している.
シミュレーションはコンピュータにより発生させられた乱数(random number)を用いて,現実世界の確かでない部分をモデル化する.当然,コンピュータは本当の乱数を発生することはできない.なぜならば,コンピュータは決定論的であるからである.しかし,乱数のようにみえる数を発生させることは可能である.つまり,ある区間で,一様分布していて,認識可能なパターンを含まない数の列(擬似乱数)を発生させることは可能である.
標準C++ライブラリ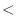 cstdlib
cstdlib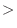 では,擬似乱数を発生させる関数rand()を定義している.rand()関数は0からRAND_MAXまでの数をランダムに発生させる.RAND_MAXも
では,擬似乱数を発生させる関数rand()を定義している.rand()関数は0からRAND_MAXまでの数をランダムに発生させる.RAND_MAXも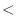 cstdlib
cstdlib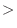 で定義されている定数である.
で定義されている定数である.
解答 擬似コードで書くと
for i=0,1,2,...,7 do
rand();
で8個の乱数を発生することができる.
|
#include <iostream>
#include <cstdlib> using namespace std; int main() { for(int i=0; i < 8;i++){ cout << rand() << endl; } cout << "RAND_MAX = " << RAND_MAX << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1460
\centering
\includegraphics[width=8.6cm]{CPPPIC/reidai4-14.eps}
\end{figure}](img106.png)
rand()関数により発生される乱数は,この例でも分かるように同じものである.なぜならば,同じ種(seed)を用いているからである.これでは,擬似乱数と呼ぶことができない.そこで,毎回違う乱数を発生させるために,srand()関数を用いて自分自身でseedを変更することができる.
解答
|
#include <iostream>
#include <cstdlib> using namespace std; int main() { unsigned seed; cout << "seedを入力して下さい:" ; cin >> seed; srand(seed); for(int i=0; i < 8;i++){ cout << rand() << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 1470
\centering\includegraphics[width=8.6cm]{CPPPIC/reidai4-15.eps}
\end{figure}](img107.png)
![\begin{figure}% latex2html id marker 1474
\centering
\includegraphics[width=8.6cm]{CPPPIC/reidai4-15-1.eps}
\end{figure}](img108.png)
解答
|
#include <iostream>
#include <cstdlib> #include <ctime> using namespace std; int main() { unsigned seed = time(NULL); cout << "seed = " << seed << endl ; srand(seed); for(int i=0; i < 8;i++){ cout << rand() << endl; } } |
実行結果
![\begin{figure}% latex2html id marker 1484
\centering
\includegraphics[width=8.6cm]{CPPPIC/reidai4-16.eps}
\end{figure}](img109.png)
解答 指定された範囲の最小値と最大値より,範囲rangeはrange = 最大値 - 最小値 + 1で求まる.次にrand()で発生させた乱数を0からrange-1までに変換するには,rand()%rangeで余りを調べればよい.
|
#include <iostream>
#include <cstdlib> #include <ctime> using namespace std; int main() { unsigned seed = time(NULL); cout << "seed = " << seed << endl ; srand(seed); int min,max; cout << "乱数の範囲の最小値と最大値を入力して下さい: "; cin >> min >> max; int range = max - min + 1; for(int i=0; i < 20;i++){ int r = rand()%range + min; cout << r << " "; } cout << endl; } |
実行結果
![\begin{figure}% latex2html id marker 1494
\centering
\includegraphics[width=13.8cm]{CPPPIC/reidai4-17.eps}
\end{figure}](img110.png)
|
練習問題 4..9
モンテカルロ法
モンテカルロ法を用いて 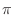 の値を求めよ.ただし,乱数の個数はRAND_MAXまでの数なら利用者が選べるようにする.0から1の間の乱数はrand()/(RAND_MAX+0.1)で発生させることができる. の値を求めよ.ただし,乱数の個数はRAND_MAXまでの数なら利用者が選べるようにする.0から1の間の乱数はrand()/(RAND_MAX+0.1)で発生させることができる. |
モンテカルロ法(Monte Carlo Method)とは,ある問題を確率(乱数)を用いて解くことをいう.
1辺が1の正方形の中に半径1の1/4円を描く.ここで,点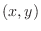 の
の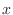 と
と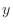 の値を0~1の一様乱数を発生させて生成すると,
の値を0~1の一様乱数を発生させて生成すると,
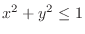 ならば,1/4円の内部にあり,それ以外は正方形の内部で,1/4円の外部にあることになる.n個の点を発生させ,1/4円の内部にばらまかれた点の数を
ならば,1/4円の内部にあり,それ以外は正方形の内部で,1/4円の外部にあることになる.n個の点を発生させ,1/4円の内部にばらまかれた点の数を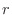 ,1/4円の外部にばらまかれた点の数を
,1/4円の外部にばらまかれた点の数を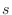 とすると,確率的に次の関係が成り立つ.
とすると,確率的に次の関係が成り立つ.
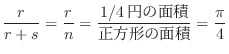
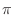 は
は
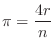
1. while文の条件式が最初から正しくない(つまり零)場合どうなるか述べよ.
2. 次のプログラムコードはどこが間違っているか.
while (n <= 100)
sum += n*n;
3. 次のプログラムコードはどこが間違っているか.
int main()
{
const double PI;
int n;
PI = 3.141592653;
n = 22;
}
4. break文はどのようにしてループにコントロールをもたらすか述べよ.
1. eを式,sを文とするとき,次のforループをwhileループを用いて書き直しなさい.
a. for(;e;)s
b. for ( ; ; e) s
2. 次のforループをwhileループを用いて書き直しなさい.
for (int i=1; i <= n; i++)
cout << i*i << " ";
3. 次のコードをトレースしなさい.
float x = 4.15;
for (int i = 0; i 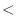 3; i++)
3; i++)
x *= 2;
4. 入力した10進数の数字を反転して出力するプログラムを書きなさい.
5. Euclidの互助法は2つの整数の最大公約数を求めるのに用いることができる.そのアルゴリズムは例えば,210と56の最大公約数ならば,
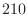 |
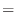 |
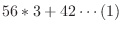 |
|
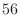 |
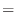 |
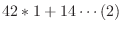 |
|
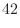 |
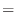 |
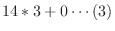 |
次に,210と56の最大公約数を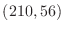 と表すと,
と表すと,