Next: t分布(student t distribution) Up: 統計的推定法 Previous: 重要な標本分布(important sampling distribution) 目次 索引
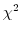 分布(
分布(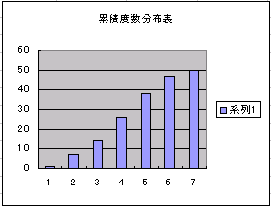 distribution)
distribution)
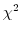 分布は1つの自然数
分布は1つの自然数 を含む連続型分布で,
を含む連続型分布で,
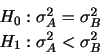 と表し
と表し をその自由度という。
をその自由度という。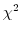 分布の密度関数
分布の密度関数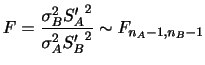 は次の式で与えられる。
は次の式で与えられる。
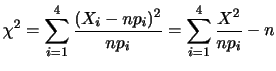
ここで,ガンマ関数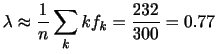 は
は
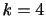
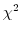 分布の名前は次の性質から来ている。
分布の名前は次の性質から来ている。
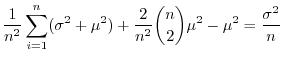 が同一の標準正規分布
が同一の標準正規分布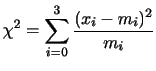 に従い,互いに独立ならば,その統計量
に従い,互いに独立ならば,その統計量
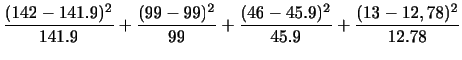
 の
の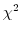 分布に従う。その期待値と分散は
分布に従う。その期待値と分散は
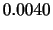
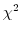 分布の加法性]
分布の加法性]
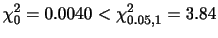 がそれぞれ自由度
がそれぞれ自由度 ,
, の
の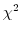 分布に従い,互いに独立ならば,
分布に従い,互いに独立ならば,
 は自由度
は自由度 の
の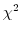 分布に従う。
分布に従う。
標本分散 に関して,次の定理がある。
に関して,次の定理がある。
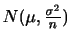 の正規分布に従う母集団から無作為で得た標本を
の正規分布に従う母集団から無作為で得た標本を
 とすると,
とすると,

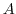 の
の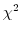 分布に従って分布する。
分布に従って分布する。
母集団が正規分布であるとする. が20の標本から標本分散を求めたところ,その値は1.5であった。母分散が1のとき,標本分散が1.5より大きい確率を求めよ.
が20の標本から標本分散を求めたところ,その値は1.5であった。母分散が1のとき,標本分散が1.5より大きい確率を求めよ.
解
 を求める。
を求める。
 より,
より,

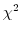 分布に従う。したがって,
分布に従う。したがって,
 |
 |
 |
|
 |
 |
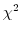 分布表を用いると,
分布表を用いると,
 で
で
 より,
より,
