next up previous contents index
: 行列の基本変形 : 行列と行列式 : 行列と行列式   目次   索引

行列

$ \spadesuit$(m,n)行列 $ \spadesuit$

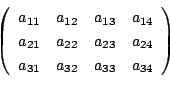
あるものの集まりをベクトル空間としてとらえることができる例として, 第1章で幾何ベクトルの集まり, 空間のベクトルの集まり, 連続関数の集まり, 区分的に連続な関数の集まりを取り上げました． その他にもたくさんベクトル空間となるものがあります．

第2章では, その中から行列とよばれている実数の配列を考えます． 数を横に並べたのを行といい, 縦に並べたのを列といいます． たとえば, 3行4列の行列は次のような形で与えられます．

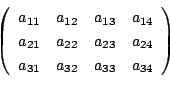
\begin{displaymath}\left( \begin{array}{llll} a_{11} & a_{12} & a_{13} & a_{14} ... ..._{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{array}\right) \end{displaymath}

ここで $ a_{ij}$ は行列の成分とよばれ, $ i$ は行の番号, $ j$ は列の番号を表しています．とくに, $ a_{ii}$ を対角成分とよびます．$ m$行$ n$列の行列を $ m \times n$型の行列といいます．また, 成分$ a_{ij}$ で構成される行列を $ A$ や$ (a_{ij})$ で表すこともあります．

行列は自然科学や社会科学の諸分野においてよく用いられています． それらの中には単なる記述法として用いられている場合もありますが, もっと幅広い利用の仕方を考えるために, ベクトル空間としてとらえる必要がでてきました． そこでまず1章で学んだように和とスカラー倍を行列に定義します．

定義 2.1   ふたつの同じ型の行列 $ A = (a_{ij})$ と $ B = (b_{ij})$ は, 対応する成分がすべて等しいとき, すなわち, すべての $ i,j$ において, $ a_{ij} = b_{ij}$ が成り立つとき, 等しいといい, $ A = B$ で表す．

$ \spadesuit$行列の和 $ \spadesuit$

行列の和はそれぞれ対応する成分どうしの和によって定義します．つまり

定義 2.2   同じ型の行列 $ A = (a_{ij})$ と $ B = (b_{ij})$ の和は $ A + B = (a_{ij} + b_{ij})$ で定義する．

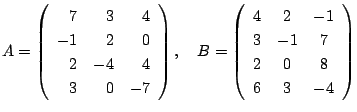例題 2.1   行列 $ A = \left ( \begin{array}{rrr} 7&3&4\\ -1&2&0\\ 2&-4&4\\ 3&0&-7 \end{array}... ...t ( \begin{array}{ccc} 4&2&-1\\ 3&-1&7\\ 2&0&8\\ 6&3&-4 \end{array}\right ) $ について, $ A +B$ を求めよう．

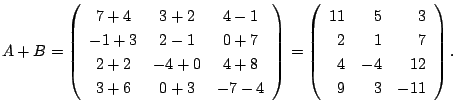
解 $ A + B = \left ( \begin{array}{ccc} 7+4&3+2&4-1\\ -1+3&2-1&0+7\\ 2+2&-4+0&4+8... ...\begin{array}{rrr} 11&5&3\\ 2&1&7\\ 4&-4&12\\ 9&3&-11 \end{array}\right ) . $ $ \blacksquare$

$ m \times n$型の行列はベクトル空間の性質1から5を満たしています．各自確かめて下さい．

$ \spadesuit$行列のスカラー倍 $ \spadesuit$

行列のスカラー倍もそれぞれの成分のスカラー倍によって定義されます．つまり

定義 2.3   行列 $ A = (a_{ij})$ の実数 $ \alpha$ によるスカラー倍 $ A\alpha = \alpha A$ は

$\displaystyle \alpha A = (\alpha a_{ij}) $

で定義する．

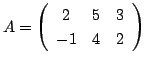例題 2.2   行列 $ A = \left ( \begin{array}{ccc} 2&5&3\\ -1&4&2 \end{array}\right ) $ について, $ 3A$ を求めよう．

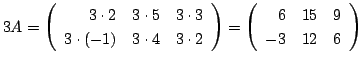解 $ 3A = \left ( \begin{array}{rrr} 3 \cdot 2 & 3 \cdot 5 & 3 \cdot 3\\ 3 \cdot (... ...{array}\right ) = \left(\begin{array}{rrr} 6&15&9\\ -3&12&6 \end{array}\right)$. $ \blacksquare$

スカラー倍はベクトル空間の性質6から9を満たしています．各自確かめてください．このことから $ m \times n$型の行列の集合をベクトル空間と考えることができます．とくに実数だけを考えているので, このベクトル空間を 実ベクトル空間(real vector space) ともいいます．しかし$ m \times n$型の行列をベクトルとよぶことはありません．例外として, $ m\times 1$型または $ 1\times n$型の行列をそれぞれ$ m$項行ベクトル(m-component row vector), $ n$項列ベクトル(n-component column vector) といいます．

$ \spadesuit$行列の積 $ \spadesuit$

和とスカラー倍に加えて行列の積も可能です．3章で勉強しますが, 行列の積は行列を写像ととらえたとき写像の合成を表します．

定義 2.4   $ A = (a_{ik}), B = (b_{kj})$ をそれぞれ$ m \times n$型, $ n\times r$型とする．行列の積(matrix multiplication)ABは $ m\times r$型の行列Cであり, 次のように表せる．

$\displaystyle C = (c_{ij}) = (\sum_{k=1}^{n} a_{ik}b_{kj}). $

他のいい方をすると, 行列Cの $ {ij}$成分は行列Aの $ i$行と行列Bの $ j$列の内積をとったものです．このことから行列 $ A$ の列の大きさと行列 $ B$ の行の大きさが等しくないと, 行列の積は定義できません．

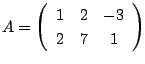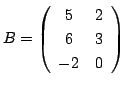例題 2.3   $ A = \left(\begin{array}{ccc} 1&2&-3\\ 2&7&1 \end{array}\right) $ と $ B = \left(\begin{array}{cc} 5&2\\ 6&3\\ -2&0 \end{array}\right) $ の積を求めよう．

解 $ A$,$ B$ の積は $ 2\times 2$型の行列でその成分は,

$\displaystyle c_{11}$ $\displaystyle =$ $\displaystyle (1)(5) + (2)(6) + (-3)(-2) = 23,$  
$\displaystyle c_{12}$ $\displaystyle =$ $\displaystyle (1)(2) + (2)(3) + (-3)(0) = 8,$  
$\displaystyle c_{21}$ $\displaystyle =$ $\displaystyle (2)(5) + (7)(6) + (1)(-2) = 50,$  
$\displaystyle c_{22}$ $\displaystyle =$ $\displaystyle (2)(2) + (7)(3) + (1)(0) = 25.$  

よって,

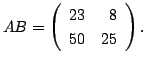
$\displaystyle AB = \left(\begin{array}{rr} 23&8\\ 50&25 \end{array}\right) .$

ついでに $ BA$ を計算すると,

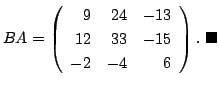
$\displaystyle BA = \left(\begin{array}{rrr} 9&24&-13\\ 12&33&-15\\ -2&-4&6 \end{array}\right). \ensuremath{ \blacksquare}$

この例題が示すように, 行列の積は交換法則が成り立たないことがあります．それどころか, $ A$ の列の数と $ B$ の行の数が違うと $ AB$ は存在すらしません．

例題 2.4   $ A \neq 0, B \neq 0$のとき, $ AB = 0$となる行列$ A,B$を求めよう．

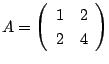
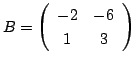解 $ A = \left(\begin{array}{cc} 1 & 2\\ 2 & 4 \end{array} \right)$ $ B = \left(\begin{array}{cc} -2 & -6\\ 1 & 3 \end{array}\right)$とおくと

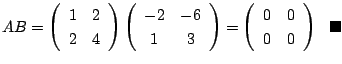
$\displaystyle AB = \left(\begin{array}{cc} 1 & 2\\ 2 & 4 \end{array}\right)\le... ...egin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right) \ensuremath{ \blacksquare}$

$ \spadesuit$行列の分割 $ \spadesuit$

行列を扱う場合, 行列をいくつかの縦線と横線で分割して考えると便利なことがあります．例えば, 次のような行列の積を考えてみましょう．

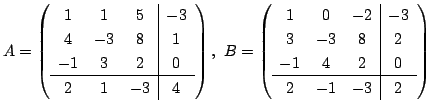
$\displaystyle A = \left(\begin{array}{ccc\vert c} 1 & 1 & 5 & -3\\ 4 & -3 & 8 ... ...\ 3 & -3 & 8 & 2\\ -1 & 4 & 2 & 0 \hline 2 & -1 & -3 & 2 \end{array}\right)$

このとき, 縦線と横線で分けられた各ブロックを小行列(sub-matrix)といいます．ここで,

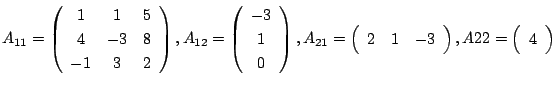
$\displaystyle A_{11} = \left(\begin{array}{ccc} 1 & 1 & 5 \\ 4 & -3 & 8 \\ -1... ...1 & -3 \end{array}\right), A{22} = \left(\begin{array}{c} 4 \end{array}\right) $

これより行列$ A$は

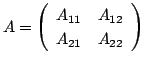
$\displaystyle A = \left(\begin{array}{cc} A_{11} & A_{12}\\ A_{21} & A_{22} \end{array}\right) $

と表すことができます．

行列$ B$を同じ方法で分割すると, 行列$ A,B$の積は

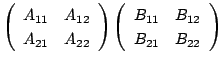$\displaystyle AB$ $\displaystyle =$ $\displaystyle \left(\begin{array}{cc} A_{11} & A_{12}\\ A_{21} & A_{22} \end{a... ...t)\left(\begin{array}{cc} B_{11} & B_{12}\\ B_{21} & B_{22} \end{array}\right)$  
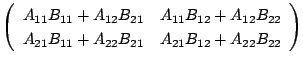  $\displaystyle =$ $\displaystyle \left(\begin{array}{cc} A_{11}B_{11} + A_{12}B_{21} & A_{11}B_{12... ...\ A_{21}B_{11} + A_{22}B_{21} & A_{21}B_{12} + A_{22}B_{22} \end{array}\right)$  

で表すことができます．

$ \spadesuit$正方行列 $ \spadesuit$

行の数と列の数が同じ行列を 正方行列(square matrix) といい, この行の数を行列の 次数(order) といいます．つまり, $ n \times n$型の行列は正方行列でその次数は $ n$ ということです．ここでこれから必要となる4種類の正方行列を紹介します．まず, 正方行列の対角成分以外の成分がすべて 0 のとき, つまり, $ a_{ij} = 0, i \neq j$ のとき, $ A$ は 対角行列(diagonal matrix)であるといいます．とくに, 対角行列のうちすべての $ i$ で $ a_{ii} = 1$ の行列を 単位行列(identity matrix) といい$ I$ で表します．たとえば,

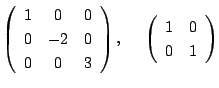
$\displaystyle \left (\begin{array}{ccc} 1&0&0\\ 0&-2&0\\ 0&0&3 \end{array}\right ), \ \left ( \begin{array}{cc} 1&0\\ 0&1 \end{array}\right ) $

は $ 3 \times 3$型の対角行列と $ 2\times 2$型の単位行列です．対角行列は和も積も対角行列となり次のような性質をもっています．

定理 2.1   $ A,B$ を $ n$ 次の対角行列とするとき, 次のことが成り立つ．
  1. $ A +B$ は対角行列である．
  2. $ AB, BA$ はともに対角行列で, $ AB = BA$ である.

証明 1. $ A = (a_{ii}), B = (b_{ii})$より、 $ A + B = (a_{ii}) + (b_{jj}) = (a_{ii} + b_{ii})$. よって$ A +B$は対角行列である。

2. $ AB = C$とおくと、

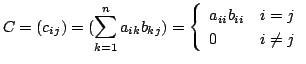
$\displaystyle C = (c_{ij}) = (\sum_{k=1}^{n} a_{ik}b_{kj}) = \left\{\begin{array}{ll} a_{ii}b_{ii} & i = j\\ 0 & i \neq j \end{array}\right.$

したがって、$ AB, BA$はともに対角行列で, $ AB = BA$ である。

$ \spadesuit$行列のトレースと転置行列 $ \spadesuit$

正方行列の対角成分の和を トレース(trace) とよび,

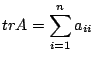
$\displaystyle tr A = \sum_{i=1}^{n} a_{ii} $

で表します．また行列 $ A$ の行と列の入れ替えによって得られる行列を 転置行列(transposed matrix) といい, $ A^{t}$ または $ {}^{t}A$ で表します．

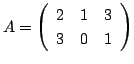例題 2.5   $ A = \left(\begin{array}{ccc} 2&1&3\\ 3&0&1 \end{array}\right ) $ のとき, $ A^{t}$ を求めよう．

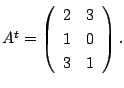
解 $ A^{t} = \left( \begin{array}{cc} 2&3\\ 1&0\\ 3&1 \end{array}\right ) .$ $ \blacksquare$

行列とその転置行列について, 次の等式が成り立ちます．

定理 2.2   行列 $ A,B$ について, 次のことが成り立つ．
  1. $ (A + B)^{t} = A^{t} + B^{t}$
  2. $ (A^{t})^{t} = A $
  3. $ (AB)^{t} = B^{t}A^{t}$

証明 1. $ A = (a_{ij})_{n \times k}, B = (b_{ij})_{n \times k}$とすると、 $ A + B = (a_{ij} + b_{ij})_{n \times k}$より、その転置行列は $ (a_{ji} + b_{ji})_{k \times n}$となる。ところで、 $ A^{t} = (a_{ji})_{k \times n}, B^{t} = (b_{ji})_{k \times n}$より、 $ (A + B)^{t} = A^{t} + B^{t}$が成り立つ。

2. $ A = (a_{ij})_{n \times k}$とすると、 $ A^{t} = (a_{ji})_{k \times n}$より、 $ (A^{t})^{t} = (a_{ij})_{n \times k} = A$.

3. $ A,B$ をそれぞれ $ n \times k, k \times m$型の行列とすると, $ AB$ は $ n \times m$型の行列となる．そして $ (AB)^{t}$ は $ m \times n$型の行列となる．転置行列の定義より, $ (AB)^{t}$ の $ (i, j)$成分は $ AB$ の $ (j, i)$成分だから $ a_{j1}b_{1i} + a_{j2}b_{2i} + \cdots + a_{jk}b_{ki}$ と表せる．また, $ B^{t}$ は $ m \times k$, $ A^{t}$ は $ k \times n$型の行列なので, $ B^{t}A^{t}$ は $ m \times n$型の行列となる．そして $ B^{t}A^{t}$ の $ (i, j)$成分は $ B^{t}$ の $ i$行と $ A^{t}$ の $ j$列の内積となるので, $ a_{j1}b_{1i} + a_{j2}b_{2i} + \cdots + a_{jk}b_{ki}$ と表せる．よって, $ (AB)^{t} = B^{t}A^{t}$. $ \blacksquare$

$ \spadesuit$対称行列 $ \spadesuit$

正方行列 $ A$ とその転置行列 $ A^{t}$ が等しいとき$ A$ は 対称行列(symmetric matrix)であるといいます．また $ A^{t} = -A$ のとき$ A$ は 交代行列(skew symmetric matrix)であるといいます．

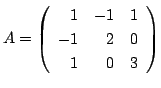例題 2.6   $ A = \left(\begin{array}{rrr} 1&-1&1\\ -1&2&0\\ 1&0&3 \end{array}\right )$ は対称行列か調べよう．

解 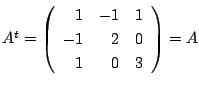$ A^{t} = \left(\begin{array}{rrr} 1&-1&1\\ -1&2&0\\ 1&0&3 \end{array}\right ) = A$より $ A$ は対称行列． $ \blacksquare$

$ n \times n$型の行列 $ A$ に対して

$\displaystyle A^{2} = AA, A^{3} = A^{2}A, \ldots , A^{n} = A^{n-1}A $

とそのベキ(power)を定義します．

$ A^{k} = 0$となる自然数$ k$が存在するとき, $ A$をベキ零行列(nilpotent)といいます．

演習問題2-2

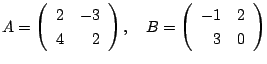1. $ A = \left(\begin{array}{rr} 2&-3\\ 4&2 \end{array}\right), B = \left(\begin{array}{rr} -1&2\\ 3&0 \end{array}\right ) $ について, 次の式を計算せよ．

(a) $ A +B$ (b) $ 2A - 3B$ (c) $ AB, BA$

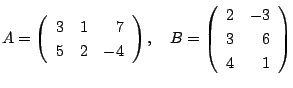2. $ A = \left(\begin{array}{rrr} 3&1&7\\ 5&2&-4 \end{array}\right), B = \left(\begin{array}{rr} 2&-3\\ 3&6\\ 4&1 \end{array}\right ) $ のとき, $ AB, BA$ を求めよ．

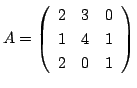3. $ A = \left(\begin{array}{rrr} 2&3&0\\ 1&4&1\\ 2&0&1 \end{array}\right)$ のとき, $ A^{2} - 5A + 6I$ を計算せよ．

4. $ A$ と $ B$ が $ n$ 次の対称行列のとき, $ A +B$ は対称行列であることを示せ．

5. $ A$ と $ B$ が $ n$ 次の対称行列のとき, $ AB$ はいつも対称行列か調べ, $ AB$ がいつも対称行列になるための必要十分条件を求めよ．

6. $ A$ が交代行列ならば, $ A^{2}$ は対称行列であることを示せ．

7. 行列 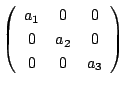$ \left(\begin{array}{ccc} a_{1}&0&0\\ 0&a_{2}&0\\ 0&0&a_{3} \end{array}\right)$ との積が交換可能な行列をすべて求めよ．ただし, $ a_{1},a_{2},a_{3}$ は相異なる実数とする．

8. 正方行列 $ A$ は, 対称行列と交代行列の和として一意的に表せることを証明せよ．

9. 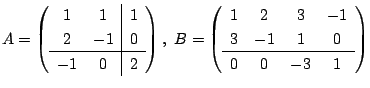$ A = \left(\begin{array}{cc\vert c} 1 & 1 & 1\\ 2 & -1 & 0 \hline -1 & 0 & 2... ...cc} 1 & 2 & 3 & -1\\ 3 & -1 & 1 & 0 \hline 0 & 0 & -3 & 1 \end{array}\right)$ の積を求めよ．

next up previous contents index
: 行列の基本変形 : 行列と行列式 : 行列と行列式   目次   索引
yokotalab 平成20年3月7日