Next: Line integral Up: Scalar field, vector field Previous: Scalar field, vector field Contents Index
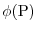 corresponds to each point
corresponds to each point 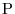 in the space area
in the space area 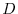 The three-variable function
The three-variable function
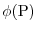 is called scalar field on
is called scalar field on 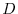 .
Similarly, in the space area
.
Similarly, in the space area 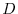 ,
when the vector
,
when the vector
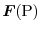 corresponds to each point
corresponds to each point 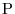 , the three-variable vector function
, the three-variable vector function
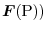 is called vector field on
is called vector field on 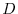 . Let the component of the vector
. Let the component of the vector
 be
be
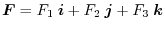 . Then
. Then
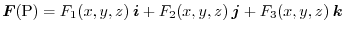
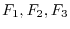 are continuous,then
are continuous,then
 is said to be continuous.
is said to be continuous.
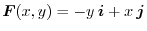 .
.
Answer
Since the vector 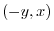 corresponds to the point
corresponds to the point 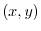 on the
on the 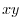 plane, a four-dimensional space is required to draw a graph. Unfortunately, a four-dimensional space cannot be prepared, so the vector field is expressed using the following method. First, select the point
plane, a four-dimensional space is required to draw a graph. Unfortunately, a four-dimensional space cannot be prepared, so the vector field is expressed using the following method. First, select the point
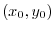 on the
on the 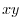 plane, and then set the vector
plane, and then set the vector
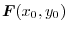 at that point. Draw the point
at that point. Draw the point
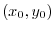 as the starting point.
as the starting point.
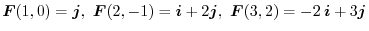
If you look at the figure 3.1, you will notice that the vector is a tangent to a curve..This curve is called streamlines or lines of force. Generally, when
 represents the velocity of a fluid, the curve drawn along the flow is called a streamline, and when
represents the velocity of a fluid, the curve drawn along the flow is called a streamline, and when
 represents a magnetic field, it is along the direction of the magnetic field. The drawn curve is called the magnetic field line..Similarly, when
represents a magnetic field, it is along the direction of the magnetic field. The drawn curve is called the magnetic field line..Similarly, when
 represents an electric field, the curve drawn along the direction of the electric field is drawn along the power line, and when
represents an electric field, the curve drawn along the direction of the electric field is drawn along the power line, and when
 represents the electromagnetic field, it is drawn along the direction of the electromagnetic field. The curved line is called an electromagnetic force line.
represents the electromagnetic field, it is drawn along the direction of the electromagnetic field. The curved line is called an electromagnetic force line.
Bring a magnet to the sandbox and collect iron sand. If you sprinkle this iron sand on paper and place a U magnet under the paper, the iron sand will line up along the lines of magnetic force, and you may have observed that the stronger the magnetic field, the more iron sand is attached. Let us consider these phenomena here..
Electric field
If the distance from the charge 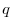 to the point P is
to the point P is 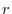 and the unit vector from
and the unit vector from 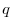 to P is
to P is
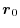 , the electric field at the point P is given by the following equation.
, the electric field at the point P is given by the following equation.
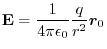
![$\epsilon_{0} = 8.85418782\times 10^{-12} [{\rm s^2C^2/kgm^2}]$](img360.png) is called the permittivity of vacuum
is called the permittivity of vacuum
Universal gravitational field
 for a universal gravitational field (generally called universal gravitational force) in which an object with a substance amount of
for a universal gravitational field (generally called universal gravitational force) in which an object with a substance amount of 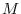 at the origin acts on an object with a substance amount of
at the origin acts on an object with a substance amount of 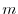 at a point P
at a point P 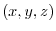 Then
Then
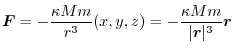
Gradient
Here, for a scalar field defined in an area of space,consider vector field
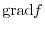 defined by
defined by
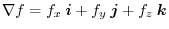
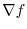 can be seen as an operator applied to
can be seen as an operator applied to 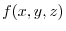 by
by
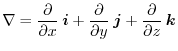
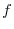 .
.
For the scalar field 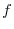 , the curved surface defined by
, the curved surface defined by
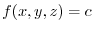 (c constant) is the level surface of the scalar field
(c constant) is the level surface of the scalar field 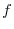 . and the group of coordinating surfaces obtained by changing the value of
. and the group of coordinating surfaces obtained by changing the value of 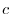 is called the coordinating surface group.
is called the coordinating surface group.
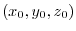 is orthogonal to the level surface through the point
is orthogonal to the level surface through the point
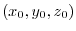 .
.
Answer
Let the level surface through the point
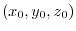 be
be
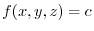
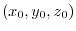 on this level surface be
on this level surface be
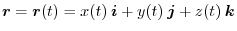
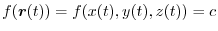 . Thus differentiate both sides by
. Thus differentiate both sides by 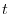 .
.
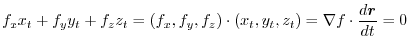
Directional derivatives
Let the unit vector 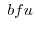 be the directional unit vector at point P. Also, a straight line passing through the point P and having
be the directional unit vector at point P. Also, a straight line passing through the point P and having 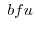 as the direction vector is represented by
as the direction vector is represented by
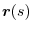 using the distance
using the distance 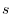 from the point P. Then, at the point P, the directional derivative of the scalar field
from the point P. Then, at the point P, the directional derivative of the scalar field 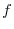 in the
in the 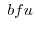 direction is given by
direction is given by
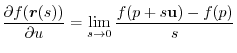
Therefore,
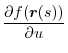 |
 |
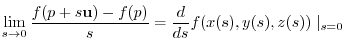 |
|
 |
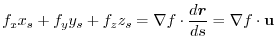 |
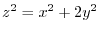 at
at 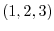 and find the directional derivative in the direction of
and find the directional derivative in the direction of 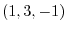 and the equation of tangent plane.
and the equation of tangent plane.
Answer Let
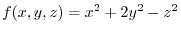
 . Also, ,
the normal vector is given by
. Also, ,
the normal vector is given by 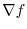 . Thus
. Thus
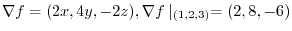
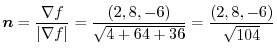
Next, find the directional unit vector to find the directional derivative in the 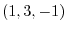 direction at the point
direction at the point 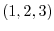 .
.
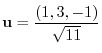 .Then the directional derivative is
.Then the directional derivative is
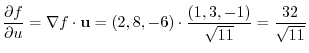
Also, the equation of the tangent plane is
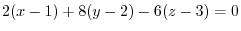 that is
that is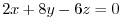
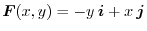 .
.
Answer
Let
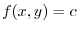 be a streamline equation. Then
be a streamline equation. Then
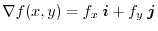 expresses the normal vector of
expresses the normal vector of
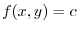 .
.
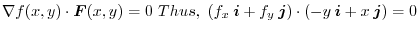
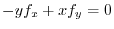 .Note that the slope of the tangent line of
.Note that the slope of the tangent line of
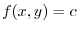 is
is
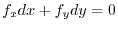 implies
implies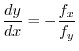
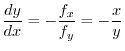
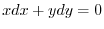 .Thus
.Thus
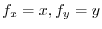 and
Next differentiate the equation 3.1 with respect to
and
Next differentiate the equation 3.1 with respect to 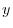 . Then
. Then
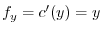 implies
implies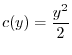
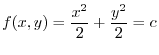
Potential
Let the position vector of the point P be
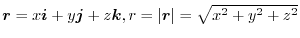 Then there are many things that are inversely proportional to the distance, such as the magnitude of universal gravitation and the intensity of light.
These can be set by
Then there are many things that are inversely proportional to the distance, such as the magnitude of universal gravitation and the intensity of light.
These can be set by
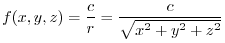
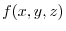 .
.
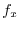 |
 |
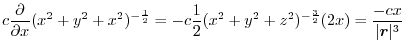 |
|
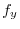 |
 |
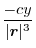 |
|
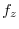 |
 |
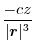 |
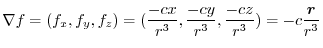
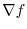 is equal to the vector field.
is equal to the vector field.
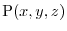 be
be
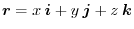 ,and vector field be
,and vector field be
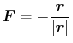 . Then show that this vector field is a conservative field in any area except at origin and
. Then show that this vector field is a conservative field in any area except at origin and
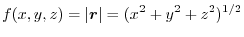
 .
.
Answer
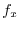 |
 |
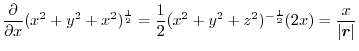 |
|
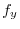 |
 |
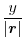 |
|
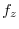 |
 |
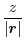 |
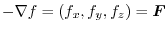 .
Thus,
.
Thus,
 is a conservative field.
is a conservative field.
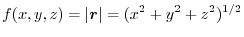
 .
.
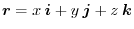 and the scalar field
and the scalar field
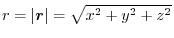 , show the followings:.
, show the followings:.
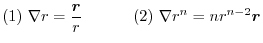
Answer (1)
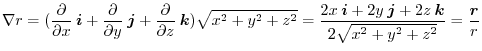
(2)
 |
 |
 |
|
 |
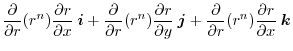 |
||
 |
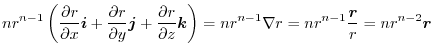 |
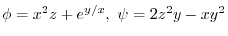 , find the followings:
(1)
, find the followings:
(1)
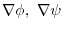
(2) the value
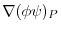 of
of
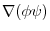 at P
at P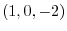 .
.
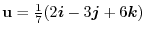 of
of
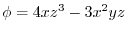 at P
at P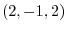 .
.
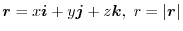 . Then find
. Then find
 ..
..
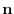 of
of
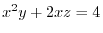 at P
at P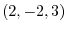 .
.
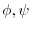 , show the followings.
, show the followings.
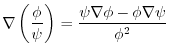
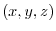 , Q
, Q
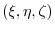 be
be 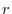 . Then prove the following for the differential operator
. Then prove the following for the differential operator