Probability axiom

1. Let

= [Throw the dice 4 times and get a 6 at least once]. $B$

= [Throw two dice 24 times at the same time and get a 6 at least once].

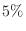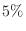2. A patient has complained of certain symptoms. From the experience of doctors, we know that about $5\%$ of people in the same age group have cancer when they complain of the condition. On the other hand, a detailed examination shows a positive reaction of $85\%$ for true cancer patients and a positive reaction of $5\%$ for non-cancer patients. If a patient gives a positive result on the work-up, find the probability that the patient has cancer.．

(a) The event $A$

's complementary event $\overline A$ , in which you throw 4 times and get a 6 at least once, will be thrown 4 times and never get a 6's. Here, the probability of not having a 6 in each time is $\displaystyle{\frac{5}{6}}$ . Then

$\displaystyle P_{r}(\overline A) = \left(\frac{5}{6}\right)^4$

$\displaystyle P_{r}(A) = 1 - P_{r}(\overline A) = 1 - \left(\frac{5}{6}\right)^4 = \frac{671}{1296}$

(b) Consider the evemt $B$

in which two dice are thrown 24 times at the same time and both rolls 6 at least once. First, when you throw two dice at the same time, the probability that both will roll a 6 is $\displaystyle{\frac{1}{36}}$ ．

Now the complement of the event $B$

is $\overline B$ and throw two dice 24 times at the same time, and both of them will not be 6 rolls. Thus,

$\displaystyle P_{r}(\overline B) = \left(1 - \frac{1}{36}\right)^{24} = \left(\frac{35}{36}\right)^{24}$

$\displaystyle P_{r}(B) = 1 - P_{r}(\overline B) = 1 - \left(\frac{35}{36}\right)^{24} = 0.491$

2 Let

「true cancer patient」， $B = $

「patients came out positive in precision inspection. Find the probability of being a cancer patient if the patient gives a positive result of the work-up．This can be expressed as follows using conditional probabilities.．

$\displaystyle P_{r}(A \vert B)$

$\displaystyle B = B \cap \Omega = B \cap (A \cup \overline A) = (B \cap A ) \cup (B \cap \overline A)$

$\displaystyle (1) \ P_{r}(B)$	$\displaystyle =$	$\displaystyle P_{r}(B \cap A) + P_{r}(B \cap \overline A) = P_{r}(A)P_{r}(B\vert A) + P_{r}(\overline A)P_{r}(B\vert\overline A)$
	$\displaystyle =$	$\displaystyle 0.05 \cdot 0.85 + 0.95 \cdot 0.05 = 0.9$
$\displaystyle (2) \ P_{r}(A \vert B)$	$\displaystyle =$	$\displaystyle \frac{P_{r}(A \cap B)}{P_{r}(B)} = \frac{P_{r}(A) P_{r}(B\vert A)}{P_{R}(B)} = \frac{P_{r}(A) P_{r}(B\vert A)}{P_{R}(B)}$
	$\displaystyle =$	$\displaystyle \frac{0.05 \cdot 0.85}{0.05 \cdot 0.85 + 0.95 \cdot 0.05} = \frac{0.425}{0.9} = 0.47$

$\displaystyle x \in \overline{A \cup B}$	$\displaystyle \Leftrightarrow$	$\displaystyle x \not\in A \cup B$
	$\displaystyle \Leftrightarrow$	$\displaystyle x \not\in A \ {\rm and} \ x \not\in B$
	$\displaystyle \Leftrightarrow$	$\displaystyle x \in \overline A \ {\rm and} \ x \in \overline B$
	$\displaystyle \Leftrightarrow$	$\displaystyle x \in \overline A \cap x \in \overline B$

$\displaystyle \overline{A \cup B} = \overline A \cap \overline B$

$\displaystyle P(\overline{A \cup B}) = P(\overline{A} \cap \overline{B})$

$\displaystyle x \in \overline{A \cap B}$	$\displaystyle \Leftrightarrow$	$\displaystyle x \not\in A \cap B$
	$\displaystyle \Leftrightarrow$	$\displaystyle x \not\in A \ {\rm or} \ x \not\in B$
	$\displaystyle \Leftrightarrow$	$\displaystyle x \in \overline A \ {\rm or} \ x \in \overline B$
	$\displaystyle \Leftrightarrow$	$\displaystyle x \in \overline A \cup x \in \overline B$