Next: Exact Differential Equations Up: 1st order linear differential Previous: Separable Differential Equations 目次 索引
2. Solve the following initial value problems.
(a)
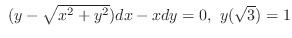
(b)
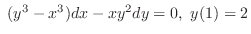
3. Example1.9 can not be solved by the method used in example1.8. Why?
Answer
1.
(a)
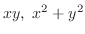 are homogeneous functions of the 2nd degree. So, divide by
are homogeneous functions of the 2nd degree. So, divide by 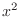 .
.
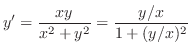
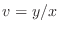 . Then
. Then
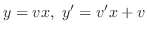 implies that
implies that
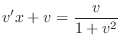
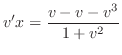
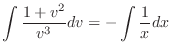
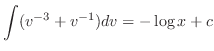
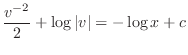
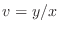 , we have
, we have
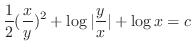
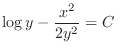
(b)
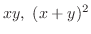 are homogeneous functions of the 2nd degree. So, divide by
are homogeneous functions of the 2nd degree. So, divide by 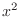 .
.
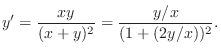
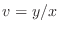 . Then
. Then
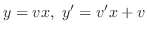 implies that
implies that
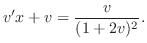
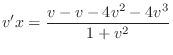
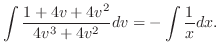
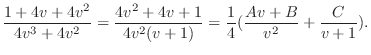
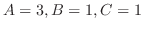 . Therefore,
. Therefore,
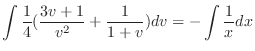
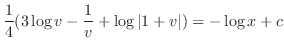
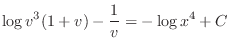
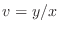 . Then
. Then
![$\displaystyle \log{[(\frac{y}{x})^{3} + (\frac{y}{x})^{4}]} - \frac{x}{y} = - \log{x^{4}} + C $](img156.png)
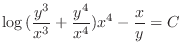
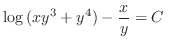
(c)
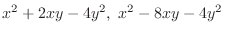 are homogeneous functions of the 2nd degree. So, divide by
are homogeneous functions of the 2nd degree. So, divide by 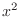 .
.
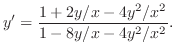
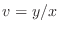 . Then
. Then
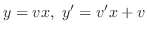 implies that
implies that
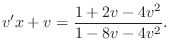
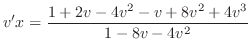
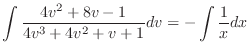
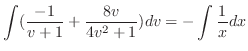
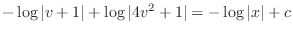
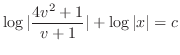
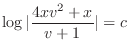
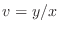 .
.
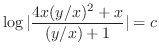
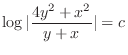
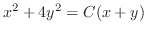
(d)
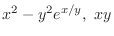 are homogeneous functions of the 2nd degree.
are homogeneous functions of the 2nd degree.
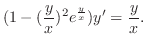
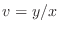 . Then
. Then
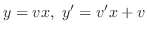 implies that
implies that
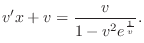
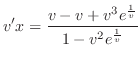
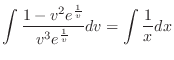
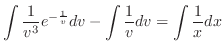
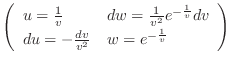
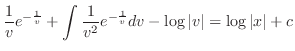
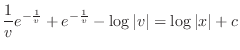
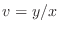 .
.
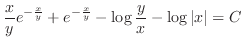
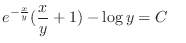
(e)
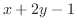 and
and
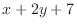 are not homogeneous functions,But they contain
are not homogeneous functions,But they contain 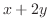 . So, we let
. So, we let
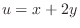 . Then
. Then
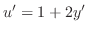 and
and
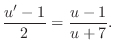
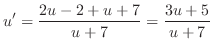
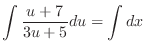
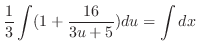
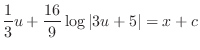
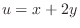 . Then
. Then
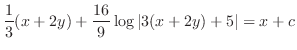
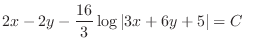
(f)
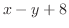 and
and
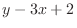 are not homogeneous functions. But once the constant term is gone, it becomes homogeneous function. So, we solve the following system of linear equations:
are not homogeneous functions. But once the constant term is gone, it becomes homogeneous function. So, we solve the following system of linear equations:
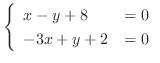
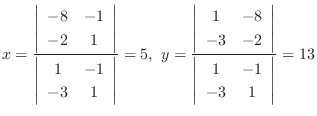
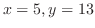 becomes the origin. Let
becomes the origin. Let
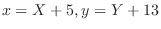 . Then we have
. Then we have
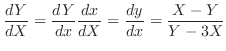
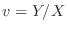 and
and
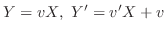 implies that
implies that
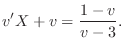
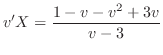
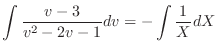
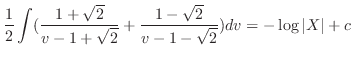
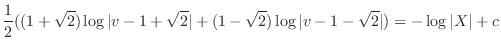
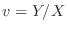 , we have
, we have
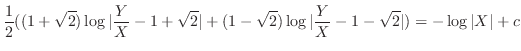
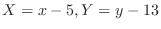 . Then
. Then
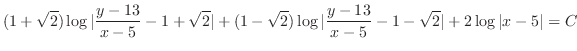
2.
(a)
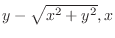 are homogeneous functions of 1st degree. So, divide by
are homogeneous functions of 1st degree. So, divide by  .
.
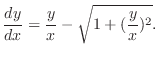
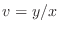 . Then
. Then
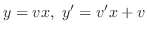 implies that
implies that
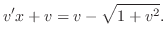
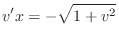
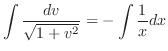
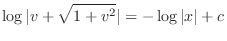
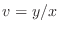 .
.
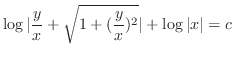
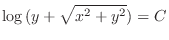
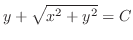
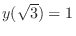 , we have
, we have
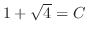 . Thus,
. Thus,
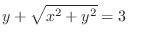
(b)
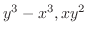 are homogeneous functions of the 3rd degree. So, divide by
are homogeneous functions of the 3rd degree. So, divide by 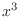 .
.
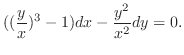
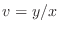 . Then
. Then
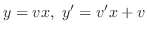 implies
implies
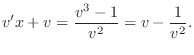
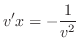
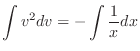
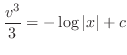
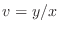 .
.
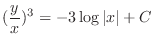
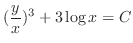
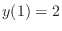 , we have
, we have 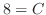 . Therefore,
. Therefore,
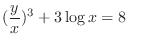
3. In example1.8, we are able to get rid of the constant term by moving the coordinates. But in example1.9, two equations
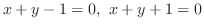 represents the parallel lines. So, we can not find the intersection.
represents the parallel lines. So, we can not find the intersection.