Next: Separable Differential Equations Up: 1st order linear differential Previous: 1st order linear differential 目次 索引
 are solutions of
are solutions of
 .
.
For
 ,find
,find
 .
.
2.. Show that
 and their linear combination is the solution of
and their linear combination is the solution of
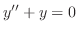 . What can you say about the spanning vector space by
. What can you say about the spanning vector space by 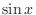 and
and  ?
?
Answer
1. Since  , we have
, we have
 .Thus,
.Thus,

 , we have
, we have
 . Thus,
. Thus,

 , we have
, we have
 . Thus,
. Thus,
 |
 |
 |
|
 |
 |
 , we find
, we find
 . Since
. Since 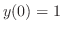 ,
,
 .Thus,
.Thus,  .
.
 implies that
implies that
 . Then
. Then
 .
.

 ,
,
 . Thus,
. Thus,

 ,
,
 . Thus
. Thus

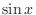 and
and  . Note that the vector space spanned by
. Note that the vector space spanned by 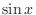 ans
ans  can be expressed by the following.
can be expressed by the following.

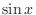 and
and  ,We now find the dimension of this vector space.
,We now find the dimension of this vector space.

 . Thus, we can say that
. Thus, we can say that 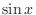 and
and  are linearly independent. Therefore,the dimension of
are linearly independent. Therefore,the dimension of
 is 2.
is 2.