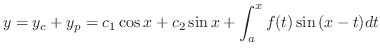Next: Linear Differential Equation with Up: Linear Differential Equations Previous: Method of Undetermined Coefficients 目次 索引
2.
Show that using variation of parameter the general solution of
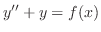 is given by
is given by
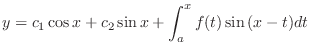
Answer
1.
(a) Given auxiliary equation
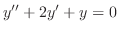 . The characteristic equation is
. The characteristic equation is
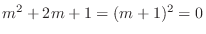 and characteristic roots are
and characteristic roots are
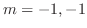 . Thus the complementary function is
. Thus the complementary function is
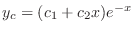
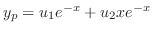
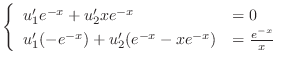
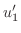 |
 |
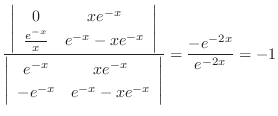 |
|
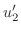 |
 |
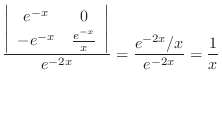 |
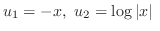 (ignore constant)
(ignore constant)
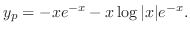
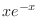 is already used in
is already used in 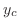 . So, we omit from
. So, we omit from 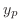 . Then the general solution is
. Then the general solution is
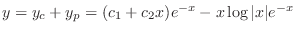
(b) Given auxiliary equation
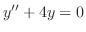 . Then the characteristic equation is
. Then the characteristic equation is
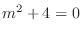 and the characteristic roots are
and the characteristic roots are
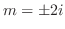 . Then the complementary function is given by
. Then the complementary function is given by
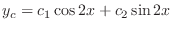
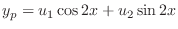
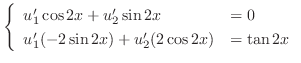
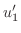 |
 |
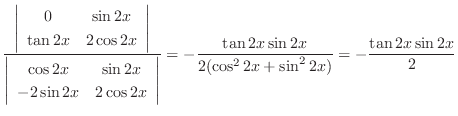 |
|
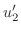 |
 |
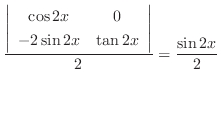 |
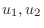 .
.
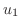 |
 |
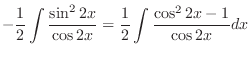 |
|
 |
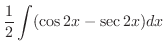 |
||
 |
 |
||
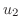 |
 |
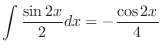 |
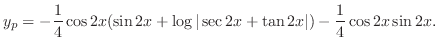
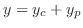 |
 |
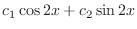 |
|
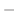 |
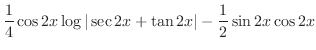 |
(c) Given auxiliary equation
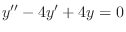 . The characteristic equation is
. The characteristic equation is
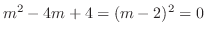 and the characteristic roots are
and the characteristic roots are 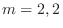 . Thus, the complementary solution is give by
. Thus, the complementary solution is give by
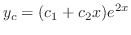
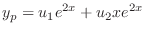
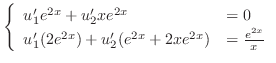
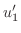 |
 |
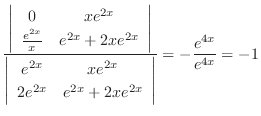 |
|
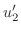 |
 |
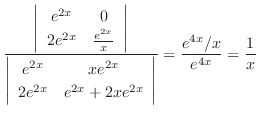 |
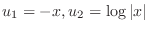 and
and
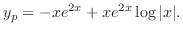
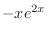 is already used in the complementary function. So, the general solution is
is already used in the complementary function. So, the general solution is
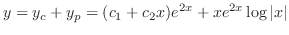
(d) Given auxiliary equation
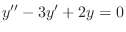 , we ahve the characteristic equation which is
, we ahve the characteristic equation which is
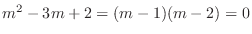 . Then the characteristic roots are
. Then the characteristic roots are 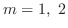 . Thus the complementary function is give by
. Thus the complementary function is give by
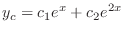
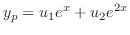
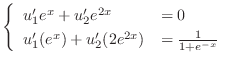
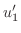 |
 |
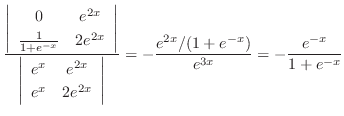 |
|
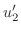 |
 |
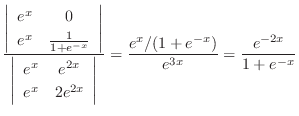 |
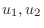 . Then
. Then
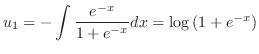
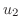 |
 |
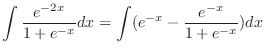 |
|
 |
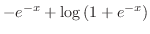 |
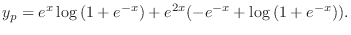
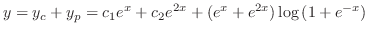
(e) The auxiliary equation is
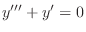 . Then the characteristic equation is
. Then the characteristic equation is
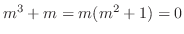 and characteristic roots are
and characteristic roots are
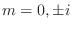 . Thus, the complementary function is given by
. Thus, the complementary function is given by
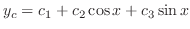
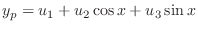
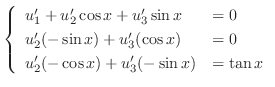
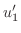 |
 |
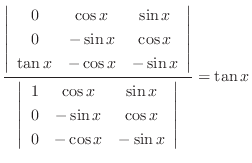 |
|
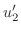 |
 |
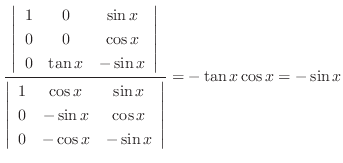 |
|
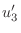 |
 |
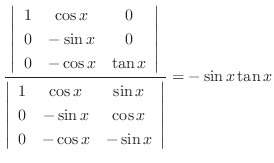 |
From this, we find
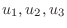 . Then
. Then
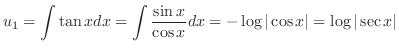
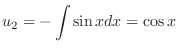
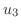 |
 |
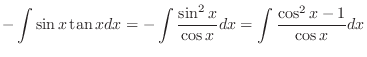 |
|
 |
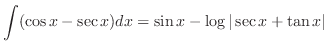 |
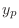 |
 |
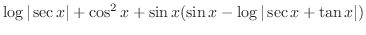 |
|
 |
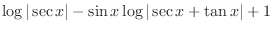 |
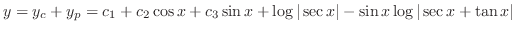
2. The auxiliary equation is
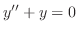 . Then the characterisitc equation is
. Then the characterisitc equation is
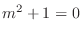 and characteristic roots are
and characteristic roots are 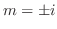 . Thus the complementary function is given by
. Thus the complementary function is given by
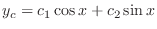
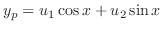
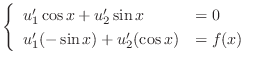
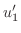 |
 |
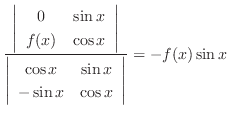 |
|
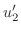 |
 |
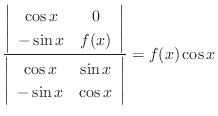 |
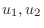 .
.
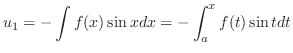
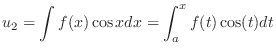
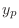 |
 |
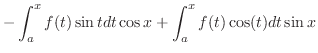 |
|
 |
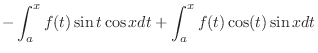 |
||
 |
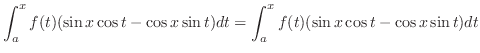 |
||
 |
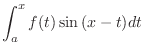 |