complex numbers and complex plane

A solution to the equation $x^2 + 1 = 0$ does not exist on ${\cal R}$ . Then, to be able to solve this equation, imaginary number $i$ is introduced. In other words, $i^2 + 1 = 0$ .

By incorporating the imaginary unit, a new system of numbers called complex number was created. Let 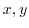$x,y$ be real numbers. Then we express $x,y \in {\cal R}$ and $x + yi$ is called a complex number.

Complex number $z = x + yi$ in orthogonal form, $z = r(\cos{\theta} + i\sin{ theta})$ is called polar form. However, $i^{2} = -1$ .

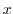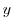$x$ of complex number $z = x + yi$ is called real part, and $x = {\rm Re}z$ , $y$ is imaginary part and it is represented by $y = {\rm Im}z$ .

When $z = x + yi$ corresponds to the point $(x,y)$ of the orthogonal coordinate form on the plane, this plane is complex plane or Gaussian plane

The absolute value of $z$ is $\vert z\vert = r = \sqrt{x^2 + y^2} \geq 0$ . The angle $\theta$ formed by the half line connecting the origin and $z$ with the real axis is called argument, and the argument is $\arg z = \theta = \tan^{-1}{\frac{y}{x}} (-\pi < \theta \leq \pi)$ .

The conjugate complex number of $z$ is represented by $\overline{z} = x - yi = r(\cos{\theta} - i\sin{\theta}) = re^{-i \theta}$ .

The operation of complex numbers is the same as the operation of real numbers, and $i^2$ can be replaced with $-1$ .

Exercise1.1

1. Show points $-3,2i,4 + i,2-2i$

on the complex plane 2. Prove the following theorem.

(a): $\bar{z_{1} + z_{2}} = \bar{z_{1}} + \bar{z_{2}}$
(b): $\bar{z_{1}z_{2}} = \bar{z_{1}}\bar{z_{2}}$
(c): $Re(z) = \frac{z + \bar{z}}{2}$

3. Prove the following inequality.

(a): $Re{z} \leq \vert z\vert$
(b): $\vert z_{1} + z_{2}\vert \leq \vert z_{1}\vert + \vert z_{2}\vert$
(c): $\vert\vert z_{1}\vert - \vert z_{2}\vert\vert \leq \vert z_{1} - z_{2}\vert$

4. Express the following complex numbers in polar form.

(a)
(b): $3 - \sqrt{3}i$
(c)
(d)

5. Draw a curve that satisfies the following equation.

(a): $\arg z =$ constant
(b): $\vert z\vert =$ constant
(c): $\vert z - 1\vert = \vert z - i\vert$
(d): $\vert z - 2i\vert = 3$
(e): $\vert z + 3\vert = 3\vert z - 1\vert$
(f): $z - \bar{z} = 2i$