Next: Complex integration Up: Analytic function,holomorphic function Previous: Analytic function,holomorphic function Index
 defined in the region
defined in the region  and a point
and a point  in
in  ,
,

 is said to be differnetiable at
is said to be differnetiable at  and this limit is denoted by
and this limit is denoted by  . Furthermore, this is called coefficient of derivative at
. Furthermore, this is called coefficient of derivative at  .
.
When all  in
in  are differentiable, the derivative
are differentiable, the derivative  is a function of
is a function of  in
in  . This is called a derivative of
. This is called a derivative of  and denoted by
and denoted by
 .
.
(1) If  are differentiable in
are differentiable in  , then the followings hold.
, then the followings hold.
(i)

(ii)

(iii)

(2) If  is differentiable in
is differentiable in  ,
,  is differentiable in
is differentiable in  , then the composite function
, then the composite function  is differentiable in
is differentiable in  and
and
 .
.
(3) If  is differentiable, then
is differentiable, then  is continuous.
is continuous.
A function
 defined in
defined in  is differentiable at
is differentiable at
 in
in  . Then keeping
. Then keeping 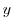 constant and bringing
constant and bringing  colser to 0, we have
colser to 0, we have

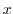 constant and bringing
constant and bringing  closer to 0, we hafe
closer to 0, we hafe



 defined in
defined in  is differentiable at
is differentiable at
 if and only if
if and only if
 is totally differentiable at
is totally differentiable at
 and satisfies
and satisfies


When  is differentiable at any point in the domain
is differentiable at any point in the domain  ,
,  is said to be analytic in
is said to be analytic in  .
.
An analytic function in  entire plane
entire plane
 is called entire function.
is called entire function.
Note1. When a function is analytic at  , it means that it is analytic including not only
, it means that it is analytic including not only  but also its neighborhood.
but also its neighborhood.
Note2. If  is analytic, it is continuous (becouse it is differentiable).
is analytic, it is continuous (becouse it is differentiable).
 is analytic in
is analytic in  and if the second partial derivatives of
and if the second partial derivatives of  are continuous, then
are continuous, then  is harmonic function. That is it satisfies Laplace's differential equation.
is harmonic function. That is it satisfies Laplace's differential equation.

Note We assumed that  and
and  have continuous second-order partial derivatives, but We don't need this assumption because the holomorphic function is separately proved to be differentiable many times.
have continuous second-order partial derivatives, but We don't need this assumption because the holomorphic function is separately proved to be differentiable many times.
 satisfies the Cauchy-Riemann's equation in the region
satisfies the Cauchy-Riemann's equation in the region  and it has a continuous partial derivatives, then
and it has a continuous partial derivatives, then
 is analytic in
is analytic in  .
. Note This theorem is a strong enough condition and effective for determining anayticity.
 ,
,
 are polynomials and its partial derivatives are continuous. Furthermore,
are polynomials and its partial derivatives are continuous. Furthermore,
 . Thus by the theorem 3.6,
. Thus by the theorem 3.6,  is analytic on whole plane.
is analytic on whole plane.
 ,
,
 . Then
. Then  and
and
 are not equal. Then the condition for anlytic in Cauchy-Riemann's equation is not satisfied. Thus,
are not equal. Then the condition for anlytic in Cauchy-Riemann's equation is not satisfied. Thus,
 is not analytic.
is not analytic.
 is analytic and
is analytic and
 , prove that
, prove that  is constant.
is constant. is analytic, by the theorem 3.4, we have
is analytic, by the theorem 3.4, we have

 . Thus,
. Thus,
 . Therefore,
. Therefore,
 are constants. Thus,
are constants. Thus,
 is also constant.
is also constant.
 is a harmonic function, and find the holomorphic function
is a harmonic function, and find the holomorphic function
 that has this in the real part.
that has this in the real part.


 implies
implies
 . Then
. Then  is a harmonic function. Next,
is a harmonic function. Next,
 is analytic. Then by Cauchy-Riemann's equation
is analytic. Then by Cauchy-Riemann's equation

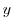 . Then
. Then

 is a function of
is a function of 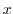 only. Put this into latter equation, we have
only. Put this into latter equation, we have
 .
Thus,
.
Thus,
 . This shows that
. This shows that
 . Therefore,
. Therefore,

(2)
 implies
implies
 ,
,
 ,
,
 ,
,
 . Then,
. Then,
 . Thus,
. Thus,  is a harmonic function. Next,
is a harmonic function. Next,
 is analytic. Then by the Cauchy-Riemann's equation, we have
is analytic. Then by the Cauchy-Riemann's equation, we have

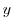 . Then
. Then

 is a function of
is a function of 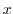 only. Now puttin this into the latter equation, we have
only. Now puttin this into the latter equation, we have
 .
Thus,
.
Thus,
 . This implies that
. This implies that
 . Therefore,
. Therefore,
 |
 |
 |
|
 |
 |
||
 |
 |



2. Differentiate the following functions.










3. When
 , check the analyticity of the following functions and if it is analytic, find the derivative.
, check the analyticity of the following functions and if it is analytic, find the derivative.



