Next: Extreme Values of Function Up: Partial Differentiation Previous: Partial Differentiation of Composite Contents Index
Suppose that partial derivatives
 are again partially differentiable with respect to
are again partially differentiable with respect to  . Then
. Then


 The second partial derivatives of
The second partial derivatives of  .
.
| Evaluation |
|---|
 , ,
 , To evaluate , To evaluate  , first differentiate with respect to , first differentiate with respect to  . .
|
If  is the class
is the class  on
on  , then
, then
 .
.
| Interchange the order |
|---|
If a function is the class  , then it is possible to interchange the order of differentiation. , then it is possible to interchange the order of differentiation.
|
 .
.
SOLUTION
 ,
,
 ,
,
 ,
,

Class  |
|---|
If  has the has the 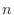 th derivatives on th derivatives on  and they are continuous, thenwe say and they are continuous, thenwe say  is the class is the class  . .
|
 for the following function.
for the following function.

SOLUTION To show
 , we first evaluate these values.
, we first evaluate these values.

 and
and
 .
Next
.
Next

 and
and
 .
.


 , show
, show
 .
.
SOLUTION
 .
.

 . Then
. Then





| Laplace Equation |
|---|
 is called two dimensional Laplace equation. is called two dimensional Laplace equation.
 is called three dimensional Laplace equation and expressed by is called three dimensional Laplace equation and expressed by  . This represents the velocity potential of the imcompressible fluid, the potential the electrostatic field, the steady state temperature distribution of the heat conduction. . This represents the velocity potential of the imcompressible fluid, the potential the electrostatic field, the steady state temperature distribution of the heat conduction.
|
SOLUTION
Let
 . Then
. Then
 |
 |
 |
|
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
 |
|
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
 |
|
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |

 2.
2.

SOLUTION 1.
 . Thus,
. Thus,
 2.
2.
 |
 |
 |
|
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
 |
|
 |
 |
 |
|
 |
 |
||
 |
 |

When we express
 by
by  . Then
. Then  is called Laplaian and the class
is called Laplaian and the class  function
function  satisfying the equation
satisfying the equation
 is called harmonic function.
is called harmonic function.

 2.
2.

| Exercise4-15-2. |
|---|

|
SOLUTION 1.
 ,
,
 ,
,
 ,
,
 .
.
Thus,

2.

 .
Thus,
.
Thus,
