Next: ANSWERS Up: Multiple Integrals Previous: Volume of Solid Contents Index
Let  be a closed bounded region in
be a closed bounded region in  space and the projection of
space and the projection of  onto
onto  -plane be
-plane be
 . Then
. Then  is expressed as
is expressed as




| Understanding |
|---|
In the triple integral, it is important to know which direction the small cuboid
 should be stacked. If the closed bounded region should be stacked. If the closed bounded region  is bounded by the two surfaces is bounded by the two surfaces
 and and
 , then it is better to stack the cuboid into the direction of , then it is better to stack the cuboid into the direction of  and in this case, and in this case,
 is innermost integral. Note that is innermost integral. Note that
 is the surface under the surface is the surface under the surface
 . .
|
NOTE Consider a small rectangular solid
 . Then as in figure5.11, fill the solid by piling up these small rectangular solid to the direction of
. Then as in figure5.11, fill the solid by piling up these small rectangular solid to the direction of  -axis.
-axis.
 , the volume of the small long rectangular solid is
, the volume of the small long rectangular solid is
 . Thus
. Thus
![$\displaystyle \iiint_{T}f(x,y,z)dxdydz = \iint_{\Omega_{xy}}[\int_{\psi_{1}(x,y)}^{\psi_{2}(x,y)}f(x,y,z)dz]dxdy.$](img1485.png)
This way, a triple integral can be reduced a double integral.
 . evaluate the following triple integrals.
. evaluate the following triple integrals.

![% latex2html id marker 29979
\includegraphics[width=3.5cm]{SOFTFIG-5/reidai5-9.eps}](img1488.png)
Pile up small rectangular solid int the direction of  , the lower surface is
, the lower surface is  and the upper surface is
and the upper surface is  .
.
SOLUTION The projection of
 onto the
onto the  -plane is the region
-plane is the region
 . Now using vertical simple region,
. Now using vertical simple region,
 Its volume is given by
Its volume is given by
 |
 |
![$\displaystyle \iint_{\Omega}\int_{z=y}^{1}dz dx dy = \int_{x=0}^{1}\int_{x}^{1} [z]_{y}^{1}dy dx$](img1494.png) |
|
 |
![$\displaystyle \int_{0}^{1}\int_{x}^{1}(1 - y)dy dx = \int_{0}^{1}\left[y - \frac{y^2}{2}\right]_{x}^{1} dx$](img1495.png) |
||
 |
![$\displaystyle \int_{0}^{1}(1 - \frac{1}{2} - (x - \frac{x^2}{2})) dx = \left[\frac{x}{2} - \frac{x^2}{2} + \frac{x^3}{6}\right]_{0}^{1}$](img1496.png) |
||
 |
 |
 , evaluate the following triple integral.
, evaluate the following triple integral.

| Exercise5-9 |
|---|
To evaluate
 , the variables other that , the variables other that  are treated as constant. are treated as constant.
![$\int_{z=y}^{1}e^{x+y+z}dz = \left[e^{x+y+z}\right]_{z=y}^{1} = e^{x+y+1} - e^{x+2y}$](img1501.png)
|
SOLUTION
The projection of
 onto
onto  -plane is the region
-plane is the region
 . Using vertical simple region,
. Using vertical simple region,
 . Thus
. Thus
 |
 |
![$\displaystyle \iint_{\Omega}\int_{z=y}^{1}e^{x+y+z}dz dx dy = \int_{x=0}^{1}\int_{x}^{1} [e^{x+y+z}]_{y}^{1}dy dx$](img1504.png) |
|
 |
 |
||
 |
![$\displaystyle \int_0^1 \left[e^{x+y+1} - \frac{1}{2}e^{x+2y}\right]_x^1 dx$](img1506.png) |
||
 |
 |
||
 |
![$\displaystyle \left[\frac{1}{2}e^{x+2} - \frac{1}{2}e^{2x+1} + \frac{1}{6}e^{3x}\right]_{0}^{1}$](img1508.png) |
||
 |
 |
||
 |
 |
 is one-to-one mapping of points in the close bounded region
is one-to-one mapping of points in the close bounded region  in
in  -space into points in the closed bounded region
-space into points in the closed bounded region  in
in  -space. Suppose that
-space. Suppose that
 are the class
are the class  and
and

 is continuous on
is continuous on  , then
, then
 |
|||
 |
 |
| Determinant |
|---|
Cofactor expansion of 1st row.

|
 be a point of the cylinder in the rectangular coordinates. Now express this by the cylindrical coordinates,
be a point of the cylinder in the rectangular coordinates. Now express this by the cylindrical coordinates,



| Check |
|---|

|
| Check |
|---|
The projection of
 onto onto  -plane is -plane is
 . .
|
 , evaluate the triple integral
, evaluate the triple integral

![% latex2html id marker 30139
\includegraphics[width=3.5cm]{SOFTFIG-5/reidai5-10.eps}](img1527.png)
SOLUTION
In the cylindrical coordinates, a point
 is expressed by the distance
is expressed by the distance  from the origin , the angle
from the origin , the angle  from the polar axis , and
from the polar axis , and  . Thus, by letting
. Thus, by letting
 ,
,
 is written as
is written as
 . a circle with the radius 1. Thus,
. a circle with the radius 1. Thus,
 and
and
 . From this, the region
. From this, the region  is mapped into the region
is mapped into the region

 |
 |
 |
|
 |
![$\displaystyle \int_{0}^{2\pi}\big( \int_{0}^{1} \big[\frac{rz}{\sqrt{1 - r^2}}\...
... = 2\pi \cdot \left[r^{2} \right ]_{0}^{1} = 2\pi \ensuremath{ \blacksquare}$](img1534.png) |
 , evaluate the following triple integral.
, evaluate the following triple integral.

| Exercise5-10 |
|---|
|
![% latex2html id marker 30182
\includegraphics[width=3.5cm]{SOFTFIG-5/enshu5-8.eps}](img1536.png)
|
SOLUTION The region  is enclosed by the cylinder
is enclosed by the cylinder
 and the surface
and the surface
 . Use the cylindrical coordinate,
. Use the cylindrical coordinate,
 . Then
. Then

 |
 |
![$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_{0}^{a}\int_0^{r\cos{\t...
...i}{2}}^{\frac{\pi}{2}}\int_{0}^{a}\left[z\right]_0^{r\cos{\theta}} r dt d\theta$](img1541.png) |
|
 |
 |
||
 |
![$\displaystyle 2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^3}{3}\right]_{0}^{a} = \frac{2a^3}{3}\ensuremath{ \blacksquare}$](img1447.png) |
 , is the distance from the origin to the point
, is the distance from the origin to the point  . The second coordinate,
. The second coordinate,  , is the angle measured from the positive
, is the angle measured from the positive  -axis. The third coordinate,
-axis. The third coordinate,  , is the angle measured from the
, is the angle measured from the  -axis. Then
-axis. Then
 Jacobian is
Jacobian is

 |
|||
 |
 |
NOTE
 , evaluate the following triple integral.
, evaluate the following triple integral.

SOLUTION
Note that the region  is the sphere of the radius 1. Now use spherical coordinates to express
is the sphere of the radius 1. Now use spherical coordinates to express
 . The angle
. The angle  is measured from the
is measured from the  -axis, so to cover the sphere,
-axis, so to cover the sphere,
 . The angle
. The angle  is measured from the
is measured from the  -axis, so to cover the sphere,
-axis, so to cover the sphere,
 . The distance
. The distance  is measured from the origin, so to cover the sphere,
is measured from the origin, so to cover the sphere,
 . Thus, the region
. Thus, the region  is mapped into the region
is mapped into the region 

 |
 |
 |
 is improper integral. So, we let
is improper integral. So, we let
 . Then
. Then
 and
and
 . Thus
. Thus
 |
 |
 |
|
 |
![$\displaystyle \int_0^{\pi/2} \frac{1 - \cos{2t}}{2}dt = \frac{1}{2}\big[t - \frac{\sin{2t}}{2}\big]_0^{\pi/2} = \frac{\pi}{4}$](img1562.png) |
 |
 |
 |
| Check |
|---|
 . .
|
 , evaluate the following triple integral.
, evaluate the following triple integral.

| Exercise5-11 |
|---|
|
![% latex2html id marker 30319
\includegraphics[width=4cm]{SOFTFIG-5/enshu5-11.eps}](img1567.png)
|
SOLUTION


 is mapped into the region
is mapped into the region
 . Then the Jacobian is
. Then the Jacobian is
 |
 |
 |
 |
 |
 |

 is mapped into
is mapped into  .
.

 |
 |
 |
|
 |
 |
 ,
,
 |
 |
 |
|
 |
 |
||
 |
 |
| Check |
|---|
![$\int_0^{\pi}\sin^{3}{\phi}\:d\phi = \int_0^\pi \sin^{2}{\phi} \sin{\phi}\:d\phi...
...hi = 2\int_0^1 (1 -t^2)\:dt = 2\left[t - \frac{t^3}{3}\right]_0^1 = \frac{4}{3}$](img1584.png)
|
 |
 |
 |
|
 |
 |
||
 |
 |
![$\int_0^{2\pi}\sin^{2}{\theta}\:d\theta = \int_0^{2\pi}\frac{1 - \cos{2\theta}}{...
...theta = \frac{1}{2}\left[\theta - \frac{\sin{2\theta}}{2}\right]_0^{2\pi} = \pi$](img1589.png)
![$\int_0^{2\pi}\cos^{2}{\theta}\:d\theta = \int_0^{2\pi}\frac{1 + \cos{2\theta}}{...
...theta = \frac{1}{2}\left[\theta + \frac{\sin{2\theta}}{2}\right]_0^{2\pi} = \pi$](img1590.png)
 |
 |
 |
|
 |
 |
||
 |
 |

Suppose the density
 . Then the mass
. Then the mass  of the solid
of the solid  is given by
is given by

 ,
,

 .
.
SOLUTION
To evaluate the triple integral, first find the projection of  onto
onto  -plane. The projection
-plane. The projection
 is the triangle region bounded by
is the triangle region bounded by
 . Now expressing by vertically simple region.
. Now expressing by vertically simple region.


![% latex2html id marker 30447
\includegraphics[width=3.5cm]{SOFTFIG-5/reidai5-12.eps}](img1602.png)
 |
|---|
If we know a surface is given by
 , then by letting , then by letting  , we can find , we can find
 . .
|
 |
 |
![$\displaystyle \iint_{\Omega_{xy}}[\int_{0}^{1-x-y}dz]dxdy = \int_{0}^{1}\int_{0}^{1-x}(1-x-y)dydx$](img1605.png) |
|
 |
![$\displaystyle \int_{0}^{1} \left[(1-x)y - \frac{y^2}{2}\right ]_{0}^{1-x} dx = \int_{0}^{1}\frac{(1-x)^{2}}{2}dx$](img1606.png) |
||
 |
![$\displaystyle - \left[\frac{(1-x)^{3}}{6}\right ]_{0}^{1} = \frac{1}{6}$](img1607.png) |

In this question, the volume is simply given by the base area  the height
the height  3. Thus
3. Thus
 .
.
 , find the mass.
, find the mass. SOLUTION

Now

 |
 |
 |
|
 |
![$\displaystyle \left[\frac{1}{2}x(1-x)y^2 - \frac{1}{3}xy^3\right ]_{0}^{1-x} = \frac{1}{6}x(1-x)^{3}$](img1616.png) |
 |
 |
 |
|
 |
![$\displaystyle \frac{1}{6}\left[\frac{1}{2}x^2 - x^3 + \frac{3}{4}x^4 -\frac{1}{5}x^5\right ]_{0}^{1} = \frac{1}{120}
\ensuremath{ \blacksquare}$](img1619.png) |
| Check |
|---|
![$\int_{0}^{1-x-y}xydz = xy\int_0^{1-x-y}dz = xy\left[z\right]_0^{1-x-y} = xy(1-x-y)$](img1620.png)
|
consider the system of 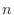 particles,
particles,
 . Now the cartesian coordinates of
. Now the cartesian coordinates of
 is
is
 and the mass of the particle
and the mass of the particle
 is
is  .
Now draw a line perpendicular to the
.
Now draw a line perpendicular to the  -axis so that the rotation moment is equal. Thus
-axis so that the rotation moment is equal. Thus



 is called centroid of a system of particles.
is called centroid of a system of particles.
If every point
 in the closed bounded region
in the closed bounded region  is given a density
is given a density
 , we partition
, we partition  into
into
 and select an arbitrary point
and select an arbitrary point
 in
in
 . Consider the centroid
. Consider the centroid
 of particles
of particles
 .
.
Let the area of
 be
be
 . Then
. Then

 ,
,
 converge to
converge to
 . Thus,
. Thus,

 represents mass.
represents mass.
If the density
 is given to each point in the closed region
is given to each point in the closed region  , we can find
, we can find
 as follows.
as follows.


 .
.
![% latex2html id marker 30591
\includegraphics[width=5cm]{SOFTFIG-5/reidai5-12.eps}](img1645.png)
SOLUTION
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle \frac{1}{m}\int_{0}^{1}\left[(\frac{x^{2}(1-x)y^{2}}{2} - \frac{x^{2}y^{3}}{3})\right ]_{0}^{1-x}dx$](img1650.png) |
||
 |
 |
||
 |
![$\displaystyle \frac{1}{6m}\left[\frac{x^{3}}{3} - \frac{3x^{4}}{4} + \frac{3x^{5}}{5} - \frac{x^{6}}{6} \right ]_{0}^{1} = \frac{1}{360m}$](img1652.png) |
 . Thus,
. Thus,
 .
.
We next find  . Interchange
. Interchange  and
and  , we get the same figure. Thus
, we get the same figure. Thus
 . Similarly,
. Similarly,


| Check |
|---|
![$\int_{0}^{1-x-y}x^2 ydz = \left[x^2y z\right]_0^{1-x-y} = x^2 y(1-x-y)$](img1658.png)
|
| Check |
|---|
![$\left[\frac{x^{2}(1-x)y^{2}}{2} - \frac{x^{2}y^{3}}{3}\right]_0^{1-x} = \frac{3...
...rac{x^2(1-x)^3}{6} = \frac{x^2(1-3x+3x^2-x^3)}{6} = \frac{x^2-3x^3+3x^4-x^5}{6}$](img1659.png)
|
 and the height
and the height  if the density at each point is constant.
if the density at each point is constant.
| Exercise5-13 |
|---|
|
![\includegraphics[width=3.5cm]{SOFTFIG-5/cone.eps}](img1661.png)
|
SOLUTION By symmetry,
 . So we only need to find
. So we only need to find  .
.

 .
Note that the triangle with the base
.
Note that the triangle with the base  and the height
and the height  and the triangle with the base
and the triangle with the base  and the height
and the height  is similar. Thus,
is similar. Thus,

 . Therefore,
. Therefore,

| Check |
|---|
|
![% latex2html id marker 30671
\includegraphics[width=2.5cm]{SOFTFIG-5/enshu5-13.eps}](img1669.png)
|
Thus
 |
 |
 |
|
 |
 |
||
 |
![$\displaystyle \int_{0}^{2\pi}\int_{0}^{a}\left[\frac{z^2}{2}\right]_{\frac{hr}{a}}^{h} r dr d\theta$](img1673.png) |
||
 |
 |
||
 |
 |
||
 |
![$\displaystyle \pi\left[\frac{h^2 r^2}{2} - \frac{h^2 r^4}{4a^2}\right]_{0}^{a} = \pi (\frac{h^2 a^2}{2} - \frac{h^2 a^4}{4a^2})$](img1676.png) |
||
 |
 |
Therefore,

Let
 be the density at each point
be the density at each point  of region. Then the moment of inertia of
of region. Then the moment of inertia of  about
about  -axis,
-axis,  -axis,
-axis,  -axis is give by the following.
-axis is give by the following.
 |
 |
 |
|
 |
 |
 |
(a) The mass of the ball
 provided the density is proportional to the distance from the origin.
provided the density is proportional to the distance from the origin.
(b) The mass of the cone  and
and
 provided that the density is proportional to the distance from the origin.
provided that the density is proportional to the distance from the origin.
(c) The volume common to
 and
and
 .
.
(a)  and
and
 provided the density is constant.
(b)
provided the density is constant.
(b)
 and
and
 .
.
(c)
 and
and
 .
.
 .
.
(a)  and
and

(b) Semishpher
 provided the density is proportional to the distanace from the origin.
provided the density is proportional to the distanace from the origin.
(c) The right circular cone with the bottom radius  and the hight
and the hight  .
.
(e) Find the center
 of the trapezoid given in Example 5.13
of the trapezoid given in Example 5.13
(f)
 provided the density is proportional to the distance from the origin.
provided the density is proportional to the distance from the origin.