next up previous
Next: Evaluation of definite integrals Up: INTEGRATION Previous: Definite integral

3.7 Answer

3.7

1.

Note that by fundamental theorem of calculus, if $f(t)$ is continuous on $[a,b]$, then for $a < x < b$,

$\displaystyle \frac{d}{dx}\int_{a}^{x}f(t)\ dt = f(x)$

$\displaystyle \frac{d}{dx}\int_{a}^{u}f(t)\ dt = \frac{d}{du}(\int_{a}^{u}f(t)\ dt)\frac{du}{dx} = f(u)\frac{du}{dx}$

(a)

$\displaystyle \frac{d}{dx}\int_{x}^{b}f(t)\ dt = \frac{d}{dx}(-\int_{b}^{x}f(t)\ dt) = -f(x)$

(b)

$\displaystyle \frac{d}{dx}\int_{x}^{x+1}f(t)\ dt$ $\displaystyle =$ $\displaystyle \frac{d}{dx}[\int_{x}^{a}f(t)\ dt + \int_{a}^{x+1}f(t)\ dt]$  
  $\displaystyle =$ $\displaystyle -f(x) + f(x+1)\frac{d(x+1)}{dx} = -f(x) + f(x+1)$  

(c)

$\displaystyle \frac{d}{dx}\int_{0}^{2x}x^{2}f(t)\ dt$ $\displaystyle =$ $\displaystyle \frac{d}{dx}(x^{2}\int_{0}^{2x}f(t)\ dt \ \left(\begin{array}{l} ... ...t}\\ x^{2}\mbox{can be taken out of the integration sign}\\ \end{array}\right)$  
  $\displaystyle =$ $\displaystyle 2x \int_{0}^{2x}f(t)\ dt + x^{2}\frac{d}{dx}\int_{0}^{2x}f(t)\ dt$  
  $\displaystyle =$ $\displaystyle 2x \int_{0}^{2x}f(t)dt + x^{2}f(2x)\cdot 2$  

2.

(a) Let $t = \sqrt{x-1}$. Then $t^2 = x-1$ and $2t dt = dx$．Then note that

\begin{displaymath}\begin{array}{llll} x&1 &\Rightarrow & 5\\ \hline t&0 &\Rightarrow & 2 \end{array}\end{displaymath}

We have
$\displaystyle \int_{1}^{5}{2\sqrt{x-1}}\ dx$ $\displaystyle =$ $\displaystyle 2\int_{0}^{2}{t(2tdt)}$  
  $\displaystyle =$ $\displaystyle 4\int_{0}^{2}t^{2}\ dt = \frac{4}{3}t^{3}\mid_{0}^{2} = \frac{32}{3}$  

(b)

$\displaystyle \int_{1}^{2}{\frac{2-t}{t^3}}\ dt$ $\displaystyle =$ $\displaystyle \int_{1}^{2}{(2t^{-3} - t^{-2})}\ dt = [-t^{-2} + t^{-1}\mid_{1}^{2}$  
  $\displaystyle =$ $\displaystyle [-\frac{1}{t^2} + \frac{1}{t}\mid_{1}^{2} = -\frac{1}{4} + \frac{1}{2} - (-1+1) = \frac{1}{4}$  

(c)


$\displaystyle \int_{0}^{\frac{\pi}{2}}{\cos{x}}\ dx$ $\displaystyle =$ $\displaystyle \sin{x}\mid_{0}^{\frac{\pi}{2}} = \sin{(\frac{\pi}{2})} - \sin{0} = 1$  

(d) Let $t = -x^{2}$. Then $dt = -2xdx$．Note that

\begin{displaymath}\begin{array}{llll} x&0 & \Rightarrow & 1\\ \hline t&0 &\Rightarrow & -1 \end{array}\end{displaymath}


$\displaystyle \int_{0}^{1}{xe^{-x^2}}\ dx$ $\displaystyle =$ $\displaystyle \int_{0}^{-1}{e^{t}(-2tdt)}$  
  $\displaystyle =$ $\displaystyle 2\int_{-1}^{0}{e^{t}}\ dt = 2e^{t}\mid_{-1}^{0} = 2(e^{0} - e^{-1}) = 2(1 - \frac{1}{e})$  

(e) Let $t = e^{x}+1$. Then $dt = e^{x} dx$．Note that

\begin{displaymath}\begin{array}{llll} x&0 & \Rightarrow & \log{2}\\ \hline t&2 &\Rightarrow & 3 \end{array}\end{displaymath}

Then
$\displaystyle \int_{0}^{\log{2}}{\frac{e^{x}}{e^{x}+1}}\ dx$ $\displaystyle =$ $\displaystyle \int_{2}^{3}{\frac{dt}{t}}\ dt = \frac{1}{a^{2}}\int{\frac{1}{\sec{t}}}$  
  $\displaystyle =$ $\displaystyle \log\vert t\vert\mid_{2}^{3} = \log{3} - \log{2} = \log{3}{2}$  

3.

4.

(a) For $0 < x < 1$ and $n > 2$, we evaluate $1 + x^{n}$. First $1 + x^{n} < 1 + x^{2}$ implies that

$\displaystyle \frac{1}{1+x^{2}} < \frac{1}{1+x^{n}}$

Also, $1 + x^{n} > 1$ implies

$\displaystyle \frac{1}{1+x^{n}} < 1$

Then

$\displaystyle \int_{0}^{1}\frac{1}{1+x^{2}}\ dx < \int_{0}^{1}\frac{1}{1+x^n}\ dx < \int_{0}^{1} 1\ dx $

Note that

$\displaystyle \int_{0}^{1}\frac{1}{1+x^2}\ dx = \tan^{-1}{x}\mid_{0}^{1} = \tan^{-1}{1} - \tan^{-1}{0} = \frac{\pi}{4}$

Thus,

$\displaystyle \frac{\pi}{4} < \int_{0}^{1}\frac{1}{1+x^n}\ dx < 1$

(b) For $0 < x < 1$ and $n \geq 1$, we evaluate $\frac{x^{n}}{1+x}$．

$\displaystyle \frac{x^{n}}{2} < \frac{x^{n}}{1+x} < x^{n}$

implies

$\displaystyle \int_{0}^{1}\frac{x^n}{2}\ dx < \int_{0}^{1}\frac{x^n}{1+x}\ dx < \int_{0}^{1} x^n\ dx $

Note that

$\displaystyle \int_{0}^{1}\frac{x^n}{2}\ dx = \frac{x^{n+1}}{2(n+1)}\mid_{0}^{1} = \frac{1}{2(n+1)}$

Also,

$\displaystyle \int_{0}^{1}x^{n}\ dx = \frac{x^{n+1}}{n+1}\mid_{0}^{1} = \frac{1}{n+1} < \frac{1}{n}$

Thus,

$\displaystyle \frac{1}{2(n+1)} < \int_{0}^{1}\frac{x^{n}}{1+x}\ dx < \frac{1}{n+1} < \frac{1}{n}$

5.

(a) Take out $\frac{1}{n}$. Then

$\displaystyle \lim_{n \to \infty}\frac{1}{n}(\frac{1}{1 + \frac{1}{n}} + \frac{1}{1 + \frac{2}{n}} + \cdots + \frac{1}{1 + \frac{n}{n}})$ $\displaystyle =$ $\displaystyle \lim_{n \to \infty}\frac{1}{n}\sum_{i=1}^{n}f(1 + \frac{i}{n})$  

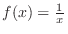Note that $f(x) = f(1 + \frac{i}{n}) = \frac{1}{1 + \frac{i}{n}}$ implies $f(x) = \frac{1}{x}$. Thus,
$\displaystyle \lim_{n \to \infty}\frac{1}{n}(\frac{1}{1 + \frac{1}{n}} + \frac{1}{1 + \frac{2}{n}} + \cdots + \frac{1}{1 + \frac{n}{n}})$ $\displaystyle =$ $\displaystyle \int_{1}^{2}\frac{1}{x}\ dx = \log\vert x\vert\mid_{1}^{2}$  
  $\displaystyle =$ $\displaystyle \log{2} - \log{1} = \log{2}$  

Alternate solution $f(x) = f(\frac{i}{n}) = \frac{1}{1 + \frac{i}{n}}$ implies $f(x) = \frac{1}{1 + x}$. Then

$\displaystyle \lim_{n \to \infty}\frac{1}{n}(\frac{1}{1 + \frac{1}{n}} + \frac{1}{1 + \frac{2}{n}} + \cdots + \frac{1}{1 + \frac{n}{n}})$ $\displaystyle =$ $\displaystyle \int_{1}^{2}\frac{1}{1+x}\ dx = \log\vert 1+x\vert\mid_{0}^{1}$  
  $\displaystyle =$ $\displaystyle \log{2} - \log{1} = \log{2}$  

(b) We take out $\frac{1}{n}$. Then

$\displaystyle \sum_{i=1}^{n}\sqrt{\frac{1}{n^{2} + i^{2}}}$ $\displaystyle =$ $\displaystyle \frac{1}{n}\sum_{i=1}^{n}\sqrt{\frac{1}{1 + (\frac{i}{n})^{2}}}$  

Note that $f(x) = f(\frac{i}{n}) = \sqrt{\frac{1}{1 + (\frac{i}{n})^{2}}}$ implies $f(x) = \sqrt{\frac{1}{1 + x^2}}$. Then
$\displaystyle \lim_{n \to \infty}\sum_{i=1}^{n}\sqrt{\frac{1}{n^{2} + i^{2}}}$ $\displaystyle =$ $\displaystyle \lim_{n \to \infty}\frac{1}{n}\sum_{i=1}^{n}\sqrt{\frac{1}{1 + (\frac{i}{n})^{2}}}$  
  $\displaystyle =$ $\displaystyle \int_{0}^{1}\sqrt{\frac{1}{1 + x^2}}\ dx$  
  $\displaystyle =$ $\displaystyle \log\vert x + \sqrt{1 + x^2}\vert\mid_{0}^{1} = \log{1 + \sqrt{2}}$  

(c)


$\displaystyle \lim_{x \rightarrow 0} \frac{\int_{0}^{x} \tan{(t^2)}dt}{x^{3}}$ $\displaystyle =$ $\displaystyle \lim_{x \to 0}\frac{\tan{x^2}}{3x^{2}}$  
  $\displaystyle =$ $\displaystyle \lim_{x \to 0}\frac{2x \sec^{2}{2x}}{6x} = \lim_{x \to 0}\frac{2\sec^{2}{2x} + 8x\sec^{2}{2x}\tan{2x}}{6}$  
  $\displaystyle =$ $\displaystyle \frac{1}{3}$  

next up previous
Next: Evaluation of definite integrals Up: INTEGRATION Previous: Definite integral