Next: Two-dimensional probability distribution Up: Random variables Previous: Random variables Contents
 that takes
that takes 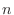 values ?such as
values ?such as
 , the probability that
, the probability that  is
is  is given,
is given,  is called random variable.
is called random variable.
 and the corresponding probability
and the corresponding probability
 is called probability distribution.
is called probability distribution.
 is taken up to a certain value
is taken up to a certain value  is expressed by
is expressed by 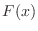 , and is called the distribution function of the random variable
, and is called the distribution function of the random variable  . Thus,
. Thus,
 .
.
If the random variable  has a finite number or an infinite number of values ??but is numbered by a natural number, the random variable
has a finite number or an infinite number of values ??but is numbered by a natural number, the random variable  is said to be discrete type. Also, if the random variable
is said to be discrete type. Also, if the random variable  can take all real numbers in an interval, it is said to be continuous type..
can take all real numbers in an interval, it is said to be continuous type..
Discrete type
The value taken by the random variable  is
is
 , and the probability of each event
, and the probability of each event
 is
is
 . Then
. Then

 is
is

 is
is
 ,the distribution function
,the distribution function  can be obtained by
can be obtained by

The probability distribution  and the distribution function
and the distribution function  have the following properties:.
have the following properties:.






Continuous type
When the random variable  takes a continuous value, the probability of the event
takes a continuous value, the probability of the event
 is determined by the continuous function
is determined by the continuous function 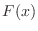 , where
, where

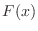 is called the distrubution function of
is called the distrubution function of  and
and 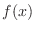 is called probability density function.
is called probability density function.
(1) Assuming that the birth rates of boys and girls are equal, find the value of the random variable  and the probability distribution
and the probability distribution  for a household with four children.
.
for a household with four children.
.
(2) One bag contains 4 red balls and 6 white balls. To take out three balls at the same time, find the random variable  and the probability distribution
and the probability distribution  , which represent the number of red balls, and draw the graph. Also, find
, which represent the number of red balls, and draw the graph. Also, find
 .
.
3. Given
 and the function
and the function

.
 for
for 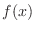 to be a probability density function?
to be a probability density function?
 for
for  , which is
, which is
 .
.
4. The probability density is given by

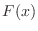 .
.
 ,
,
 .
.
5. A function is given by

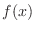 gives a probability density function.
gives a probability density function.
 so that
so that
 ,
,
 .
.
1. Let  be the number of boys in a household with 4 children,Then
be the number of boys in a household with 4 children,Then





 is given by
is given by

2. There are
 combinations for extracting 3 out of 10. Also, the fact that red is zero out of three means that white is the same as three, so three are taken out from six whites, and the combination is
combinations for extracting 3 out of 10. Also, the fact that red is zero out of three means that white is the same as three, so three are taken out from six whites, and the combination is
 . Therefore, if
. Therefore, if  is the number of red balls,
is the number of red balls,




3.
(a) For 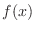 to be a probability density function, we need to show the followings are satisfied.
to be a probability density function, we need to show the followings are satisfied.


Then,
1. If the constant  is 0 or more,
is 0 or more,
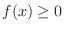 is satisfied.
is satisfied.
2.
 . Then we set
. Then we set
 .
.

(4)
(a) Note that the distribution function 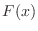 is given by
is given by
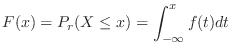
For  ,
,

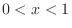 ,
,
 |
 |
 |
|
 |
![$\displaystyle 0 + \left[3t^2 - 2t^3\right]_{0}^{x} = 3x^2 - 2x^3$](img255.png) |
 ,
,

 |
 |
![$\displaystyle P_{r}(0 < X \leq 0.7) = F(0.7) - F(0) = \left[F(x)\right]_{0}^{0.7}$](img259.png) |
|
 |
![$\displaystyle \left[3x^2 - 2x^3\right]_{0}^{0.7} = 3(0.7)^2 - 2(0.7)^3$](img260.png) |
 |
 |
![$\displaystyle \left[F(x)\right]_{0.2}^{0.8} = \left[3x^2 - 2x^3\right]_{0.2}^{0.8}$](img262.png) |
|
 |
 |
4.
We need to show
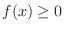 and
and
 .
.
1.
 is exponential function. So, for all
is exponential function. So, for all  ,
,  .
.
2.
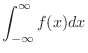 |
 |
 |
|
 |
 |
||
 |
![$\displaystyle \left[0 + -e^{-x} \right]_{0}^{\infty -} = 1$](img269.png) |

 .Therefore,
.Therefore,


 that satisfies
that satisfies
 is
is
