Next: Elementary Row Operation Up: Matrix and Determinant Previous: Matrix and Determinant Contents Index



As an example of vector space, we considered a set of geometric vectors in 1, a set of space vectors, a set of continuous functions, and a set of piecewise continuous functions.
In chapter 2, we treat a rectangular array of real numbers.
A horizontal  -tuple is called row and a vertical
-tuple is called row and a vertical 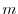 -tuples is called column. For example,
-tuples is called column. For example,
 matrix is given in the following form.
matrix is given in the following form.

 th entry
th entry 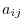 is called a component,
is called a component, 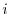 is a row number and
is a row number and 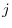 is a column number. Especially,
is a column number. Especially,  are called diagonal components. A matrix with
are called diagonal components. A matrix with 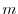 rows and
rows and  columns is called an
columns is called an
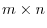 matrix; the pair of numbers
matrix; the pair of numbers  is called its size or shape. Also, a mtrix with
is called its size or shape. Also, a mtrix with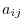 components is denoted by
components is denoted by  or
or 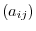 .
.
Matrices are often used in a natural science or a social science. Matrices are need to be considered as a mathematical objects. To do so, we define an addition and a scalar multiplication.
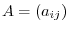 and
and
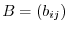 , if corresponding components are the same; for every
, if corresponding components are the same; for every  ,
,
 . Then
. Then  .
.
 Matrix Additon
Matrix Additon

A matrix addition is defined by additing corresponding entries.
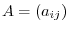 and
and
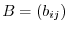 be two matrices with the same size. Then the sum of
be two matrices with the same size. Then the sum of  and
and  , written
, written  is defined
is defined
 .
.
 , find
, find  .
.
Answer


Note that for matrices with
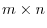 satisfy the properties 1 thru 5 of a vector space. We recommend everyone to check it.
satisfy the properties 1 thru 5 of a vector space. We recommend everyone to check it.
 Scalar Multiplication
Scalar Multiplication

A scalar multiplication is defined by multiplying each entry by the scalar.
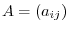 by a scalar
by a scalar  , written
, written
 is defined
is defined

 . Find
. Find  .
.
Answer
 .
.

A scalar multiplication of matrices satisfies the properies 6 thru 9 of the vector space. From this fact, we can think of a set of
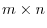 matrices as a vector space. When the entries are all real numbers, it is called real vector space. But we never say an
matrices as a vector space. When the entries are all real numbers, it is called real vector space. But we never say an 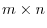 matrix a vector. As an exception,
matrix a vector. As an exception,  matrix or
matrix or  matrix are called m-component row vector or n-component column vector.
matrix are called m-component row vector or n-component column vector.
Matrix Multiplication
Besides an addition and a scalar multiplication, it is possible to define a multiplicaiton of matrices. In the chapter 3, we study that a multiplication of two matrices represents a composition of transformations.
 be
be 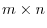 matrix and
matrix and  matrix. Then the matrix multiplication
matrix. Then the matrix multiplication 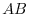 is
is  matrix
matrix  such that
such that

In other words, an  components of
components of  is given by taking inner product of
is given by taking inner product of 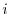 th row of the matrix
th row of the matrix  and a
and a 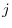 th column of the matrix
th column of the matrix  . From this, when you take a matrix multiplication of
. From this, when you take a matrix multiplication of  and
and  , the size of row of
, the size of row of  and the size of column of
and the size of column of  must be same.
must be same.
 and
and
 .
.
Answer
The product of two matrices  and
and  is
is  matrix with the components,
matrix with the components,
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |

 , then
, then

As you can see, the operation of product of matrices is not commutative. In other words,
 .
.
 , find matrices
, find matrices  and
and  so that
so that  .
.
Answer

 とおくと
とおくと

 Block Matrices
Block Matrices

Using a system of horizontal and vertical lines, we can partition a matrix  into smaller matrices called blocks of
into smaller matrices called blocks of  , The matrix
, The matrix  is then called a block matirx.
is then called a block matirx.
Consider matrices  and
and  .
.

Each block divided by the horizontal and vertical lines is called sub-matrix, Here we let

 can be written
can be written

Next we divide  same as
same as  . The the product of matrices
. The the product of matrices  and
and  is given by the followings:
is given by the followings:
 |
 |
 |
|
 |
 |
 Square Matrices
Square Matrices

A matrix with the same number of rows as columns is called a square matrix. the number of rows and columns of the square matrix is called order. In other words, An
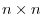 is a square matrix with the order
is a square matrix with the order  .
.
Now we introduce four different kind of square matrices.
1. A square matrix with the diagonal entries are all 0. i.e., For
 ,
,  is called diagonal matrix.
is called diagonal matrix.
2. A square matrix with
 for all
for all 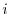 and
and
 for all
for all  is called identity matrix and denoted by
is called identity matrix and denoted by 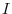 .
.

 is an diagonal matrix with
is an diagonal matrix with
 and
and  is a identity matrix of
is a identity matrix of

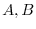 be diagonal matrices of order
be diagonal matrices of order  . Then show the followings:
. Then show the followings:
 is a diagonal matrix.
is a diagonal matrix.
 are diagonal matrices and
are diagonal matrices and  .
.
Proof
1. Let
 . Then
. Then
 . Thus
. Thus  is a diagonal matrix。
is a diagonal matrix。
2. Let  . Then
. Then

 are diagonal matrices and
are diagonal matrices and  .
.
 Transposed Matrix
Transposed Matrix

The sum of a diagonal entries is called trace and denoted by

 , written
, written 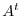 , is the matrix obtained by writing the rows of
, is the matrix obtained by writing the rows of  , in order, as columns.
, in order, as columns.
 . Find
. Find 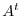 .
.
Answer


The transpose operation on matrices satifies the following properties:
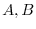 , the followings hold.
, the followings hold.



Proof
1. Let
 . Then
. Then
 . Thus the transposed matrix is given by
. Thus the transposed matrix is given by
 . On the other hand,
. On the other hand,
 . Thus we have
. Thus we have
 .
.
2. Let
 . Then
. Then
 . Thus,
. Thus,
 .
.
3.
Let 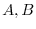 be
be
 matrices. Then the matrix
matrices. Then the matrix 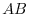 is the size of
is the size of
 . Also,
. Also,  is the size of
is the size of
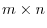 . By the definition of transposed matrix,
. By the definition of transposed matrix,  element of
element of  is the
is the  element of
element of 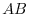 . So,
. So, 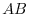 can be expressed as
can be expressed as
 . Now
. Now  is the order fo
is the order fo
 and
and 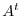 is the order of
is the order of
 . Thus,
. Thus,
 is the order of
is the order of
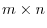 .
.  element of
element of
 is the inner product of
is the inner product of 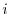 th row of
th row of  and
and 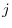 th column of
th column of 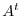 . Thus,
. Thus, 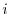 th row and
th row and 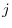 th column of the matrix
th column of the matrix
 is
is
 . Therefore,
. Therefore,
 .
.

 Symmetric Matrices
Symmetric Matrices

When the square matrix  and its transpose matrix
and its transpose matrix 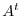 are the same, we say
are the same, we say  is symmetric matrix.
When the matrix
is symmetric matrix.
When the matrix  satisfies
satisfies
 , we say
, we say  is skew symmetric matrix.
is skew symmetric matrix.
 is a symmetric matrix.
is a symmetric matrix.

Answer
 . Thus
. Thus  is a symmetric matrix.
is a symmetric matrix.

For the square matrix  with the order of
with the order of
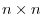 . We define the power as follows:
. We define the power as follows:

When the matrix  satifies
satifies  for some natural number
for some natural number 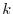 , we say the matrix
, we say the matrix  is nilpotent.
is nilpotent.
1. For matrices
 , evaluate the followings:
, evaluate the followings:
2. For matrices
 , find
, find  .
.
3. For the matrix
 , calculate
, calculate
 .
.
4. Let  and
and  be symmetric matrices of the order
be symmetric matrices of the order  . Show that
. Show that  is a symmetric matrix.
is a symmetric matrix.
5. Let  and
and  be symmetric matrices of the order
be symmetric matrices of the order  . Find the necessary and sufficient conditions so that
. Find the necessary and sufficient conditions so that 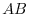 is a symmetric matrix.
is a symmetric matrix.
6. Suppose that  is a skew symmetric matrix. Then show that
is a skew symmetric matrix. Then show that  is a symmetric marix.
is a symmetric marix.
7. Find matrices so that the product of
 is interchangeable. Here,
is interchangeable. Here,
 are different real numbers.
are different real numbers.
8. Show that any square matrix  can be expressed by the sum of a symmetric matrix and a skew symmetric matrix.
can be expressed by the sum of a symmetric matrix and a skew symmetric matrix.
9. Find the product of  and
and  , where
, where
 .
.