Next: 5.2 Residue Up: Solution Previous: 4.4 Cauchy's integral formula Index
1. Laurent expansion around 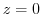 is expressed by
is expressed by
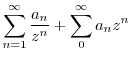
To find Laurent expansion, it is useful to know the following Taylor expansion..
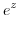 |
 |
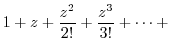 |
|
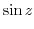 |
 |
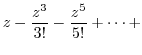 |
|
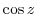 |
 |
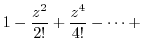 |
|
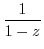 |
 |
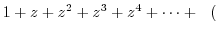 here here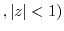 |
(a) Since 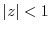 ,
,
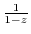 can be Taylor expanded. First we expand
can be Taylor expanded. First we expand
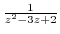 by using partial fraction expansion. Then
by using partial fraction expansion. Then
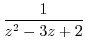 |
 |
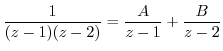 |
|
 |
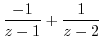 |
Note that
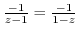 . Then
. Then
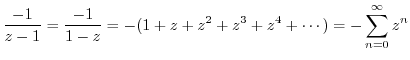
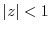 , we write
, we write
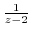 by
by
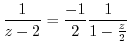
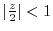 . Then we can use Taylor expansion.
. Then we can use Taylor expansion.
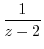 |
 |
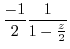 |
|
 |
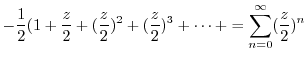 |
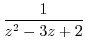 |
 |
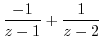 |
|
 |
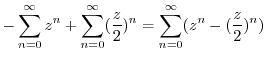 |
||
 |
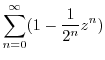 |
(b) Since
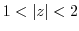 ,
,
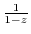 can not be Taylor expanded. But if we write
can not be Taylor expanded. But if we write
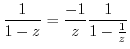
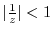 . Thus we can use Taylor expansion.
We expand
. Thus we can use Taylor expansion.
We expand
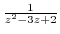 using partial fraction expansion.
using partial fraction expansion.
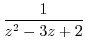 |
 |
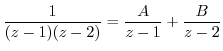 |
|
 |
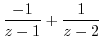 |
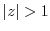 , we write
, we write
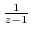 by
by
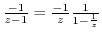 .
.
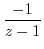 |
 |
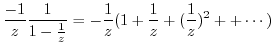 |
|
 |
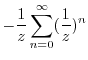 |
||
 |
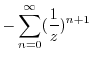 |
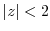 , we write
, we write
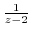 by
by
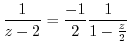
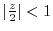 . Then we can use Taylor expansion.
. Then we can use Taylor expansion.
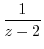 |
 |
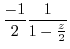 |
|
 |
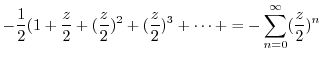 |
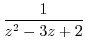 |
 |
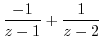 |
|
 |
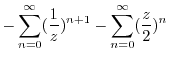 |
(c) Since 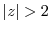 ,
,
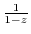 can not be Taylor expanded. But if we write
can not be Taylor expanded. But if we write
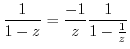
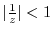 . Thus it can be Taylor expanded.
We expand
. Thus it can be Taylor expanded.
We expand
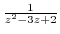 using partial fraction expansion.
using partial fraction expansion.
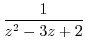 |
 |
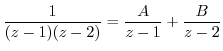 |
|
 |
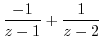 |
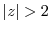 , we write
, we write
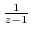 by
by
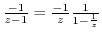 .
.
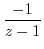 |
 |
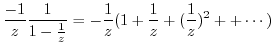 |
|
 |
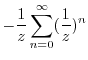 |
||
 |
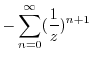 |
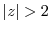 , we write
, we write
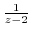 by
by
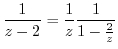
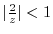 . Then it can be Taylor expanded. Thus
. Then it can be Taylor expanded. Thus
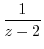 |
 |
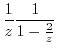 |
|
 |
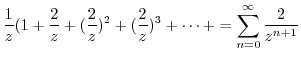 |
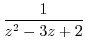 |
 |
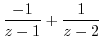 |
|
 |
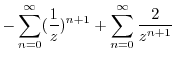 |
||
 |
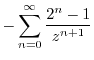 |
2.
(a) Since it is a Laurent expansion with 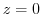 , we do not do anything with
, we do not do anything with
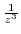 . Thus we expand
. Thus we expand
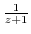 using Taylor expansion. Then
using Taylor expansion. Then
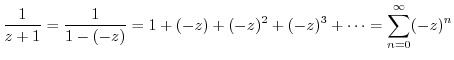
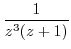 |
 |
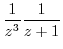 |
|
 |
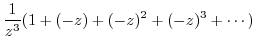 |
||
 |
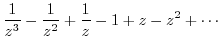 |
Note that the singularity 0 is the 3rd pole.
(b) For Laurent expansion of 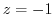 , let
, let 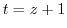 . Then
. Then
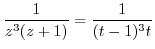
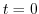 .
Now we have nothing to do with
.
Now we have nothing to do with
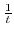 . Thus, we expand
. Thus, we expand
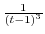 using Taylor expansion. Then
using Taylor expansion. Then
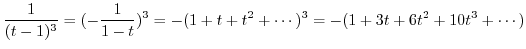
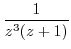 |
 |
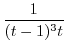 |
|
 |
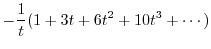 |
||
 |
![$\displaystyle -[\frac{1}{t} + 3 + 6t + 10t^2 + \cdots]$](img814.png) |
||
 |
![$\displaystyle -[\frac{z+1} + 3 + 6(z+1) + 10(z+1)^2 + \cdots]$](img815.png) |
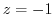 is the 1st pole.
is the 1st pole.
(c) For a Laurent expansion with 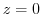 , we have nothing to do with
, we have nothing to do with
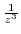 . Then expand
. Then expand 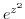 using Taylor expansion.
using Taylor expansion.
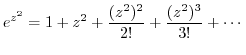
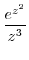 |
 |
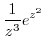 |
|
 |
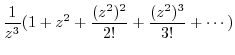 |
||
 |
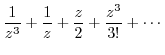 |
Note that the singularity 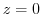 is the 3rd pole.
is the 3rd pole.
(d) For a Laurent expansion with 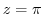 , let
, let 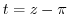 . Then
. Then
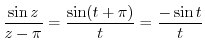
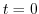 .
.
Note that we have nothing to do with
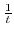 . Thus expand
. Thus expand 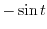 using Taylor expansion.
using Taylor expansion.
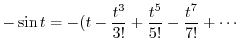
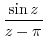 |
 |
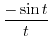 |
|
 |
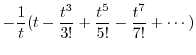 |
||
 |
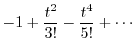 |
||
 |
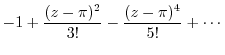 |
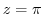 is removal singularity.
is removal singularity.