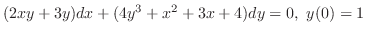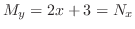Next: 演習問題 Up: 1階微分方程式 Previous: 演習問題 目次 索引
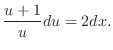 の全微分は
の全微分は
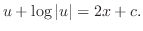
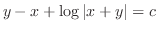 がわかれば,全微分
がわかれば,全微分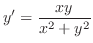 が求まります.逆に,関数の全微分がわかると次の例題が示すように,その関数を任意の定数の範囲できめることができます.
が求まります.逆に,関数の全微分がわかると次の例題が示すように,その関数を任意の定数の範囲できめることができます.
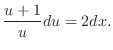 の全微分は
の全微分は
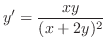
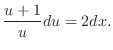 を求めよ.
を求めよ.
解
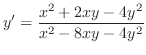 と
と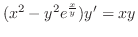 の係数は
の係数は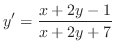 と
と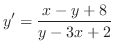 である.したがって
である.したがって
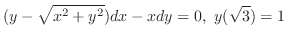
 について積分すると
について積分すると
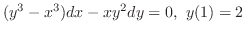
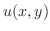 は
は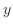 についての任意関数(なぜ?).この式を
についての任意関数(なぜ?).この式を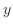 について偏微分すると
について偏微分すると
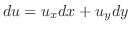
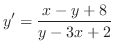 と最初に与えられた
と最初に与えられた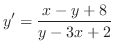 は等しいはずであるから,
は等しいはずであるから,
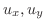
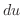 となり,
となり,
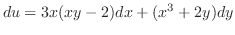 を得る.ただし
を得る.ただし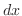 は任意定数.よって
は任意定数.よって
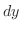

次の定義は全微分と完全微分形微分方程式を結びつけてくれます.
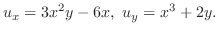 を解け.
を解け.
解
例題1.10で上の微分方程式の左辺が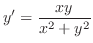 と等しい関数
と等しい関数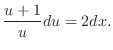 を求めた.よって一般解は
を求めた.よって一般解は
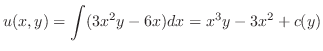
次の定理は与えられた微分方程式が完全微分形か,でないか簡単にテストする方法を示唆しています.
|
定理 1..1
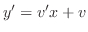 と と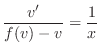 の の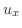 階の偏導関数が,ある領域 階の偏導関数が,ある領域
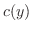 上で連続であるとする.そのとき,次の条件は同値である. 上で連続であるとする.そのとき,次の条件は同値である.
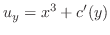 は完全微分形である は完全微分形である
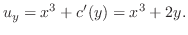 |
証明
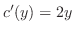
微分方程式が完全微分形ならば,
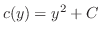 となる関数
となる関数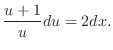 が存在する.よって
が存在する.よって
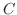
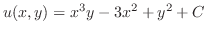 を
を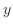 で偏微分,
で偏微分,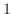 を
を で偏微分すると
で偏微分すると
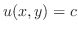
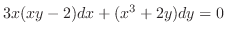 は仮定より連続なので
は仮定より連続なので
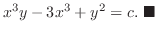 も連続である.よって微積分学で学んだSchwartzの定理(Schwarz lemma)より
も連続である.よって微積分学で学んだSchwartzの定理(Schwarz lemma)より
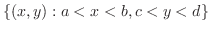 となり,
となり,
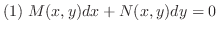 を得る.
を得る.
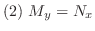
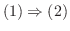 を
を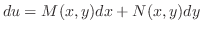 の定義域に属する点とする.
まず,
の定義域に属する点とする.
まず,
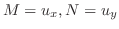 より
より
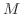
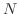 を満たすように,つまり
を満たすように,つまり
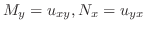
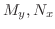 を定めればよい.
を定めればよい.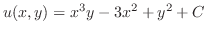 は連続な偏導関数をもつから,微分と積分の順序の交換ができて
は連続な偏導関数をもつから,微分と積分の順序の交換ができて
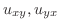
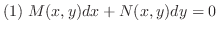 より
より
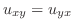 |
 |
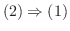 |
|
 |
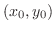 |
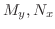 は
は
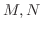
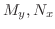 を
を
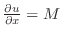
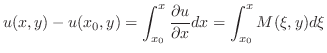
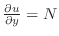
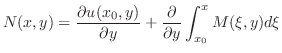 は完全微分形である.
は完全微分形である.

この定理の証明の中に完全微分形のときの解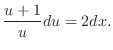 が与えられています.つまり
が与えられています.つまり
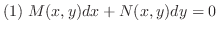 のとき,一般解は
のとき,一般解は
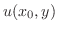
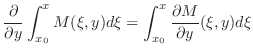 を解け.
を解け.解
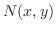

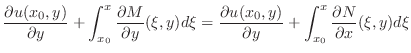 として一般解を求めると
として一般解を求めると
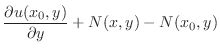 |
 |
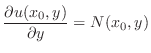 |
|
 |
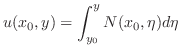 |
||
 |
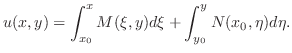 |
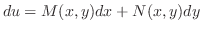
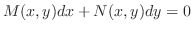 を解け.
を解け.
解
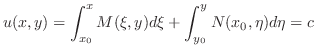 より,方程式は完全微分形である.よって
より,方程式は完全微分形である.よって
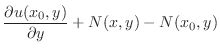 |
 |
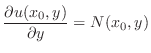 |
|
 |
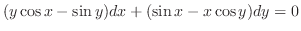 |
||
 |
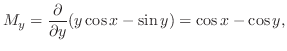 |
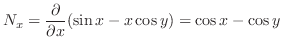
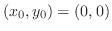 より
より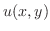 が定まる.
が定まる.

公式
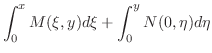 を用いて,一般解を求める方法の他に,もっとよく用いられている方法にくくり直し法(grouping method)とよばれているものがあります.この方法を次の例題を用いて説明します.
を用いて,一般解を求める方法の他に,もっとよく用いられている方法にくくり直し法(grouping method)とよばれているものがあります.この方法を次の例題を用いて説明します.
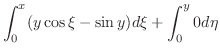 を解け.
を解け.
解
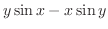 より,方程式は完全微分形である.そこで
より,方程式は完全微分形である.そこで
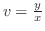 を
を