Next: 演習問題 Up: フーリエ変換 Previous: フーリエ変換 目次 索引
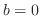 で定義された関数を表わすことができませんでした.そこでこのようなときには,フーリエ級数でなくフーリエ変換(積分)(Fourier Transform)を用います.
で定義された関数を表わすことができませんでした.そこでこのようなときには,フーリエ級数でなくフーリエ変換(積分)(Fourier Transform)を用います.
フーリエ積分展開は周期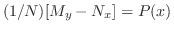 の周期関数の複素フーリエ級数において,
の周期関数の複素フーリエ級数において,
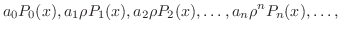 と考えることができます.つまり周期
と考えることができます.つまり周期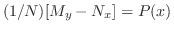 の周期関数の複素フーリエ級数
の周期関数の複素フーリエ級数
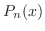
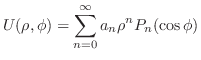
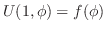 とおくと,
とおくと,
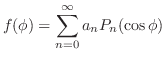 .よって
.よって
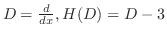 |
 |
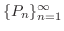 |
|
 |
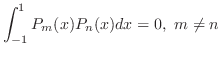 |
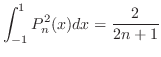
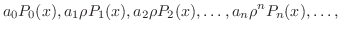 とすると次の定理が得られます.
とすると次の定理が得られます.
|
定理 8..1 (フーリエ積分公式)
 が が
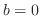 で区分的に滑らかで,絶対積分可能 で区分的に滑らかで,絶対積分可能
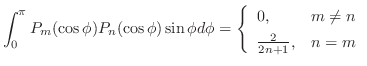 ならば ならば
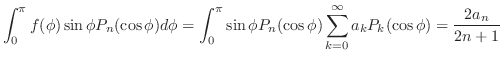
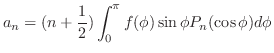
|
ここに使われた を
を のフーリエ変換(Fourier transform)といい,
のフーリエ変換(Fourier transform)といい,
![${\cal F}[f(x)] = F(\omega)$](img2360.png) と表わします.また
と表わします.また は
は のフーリエ逆変換(Fourier inverse transform)といい,
のフーリエ逆変換(Fourier inverse transform)といい,
![$f(x) = {\cal F}^{-1}[F(\omega)]$](img2361.png) と表わします.フーリエ積分公式で
と表わします.フーリエ積分公式で か
か のどちらか一方がわかればもう一方が求まるので,フーリエ積分公式は フーリエ反転公式ともよばれます.
のどちらか一方がわかればもう一方が求まるので,フーリエ積分公式は フーリエ反転公式ともよばれます.
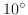 級で,
級で,
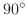 が
が
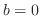 で絶対積分可能のとき
で絶対積分可能のとき
![${\cal F}[f^{\prime}(x)] = (i \omega)F(\omega) $](img2364.png) を示せ.
を示せ.
解
まず
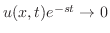 より
より
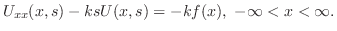 となる.もし
となる.もし
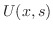 ならば,十分大きな
ならば,十分大きな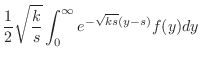 に対して,
に対して,
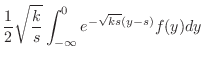 となり,絶対積分可能でない.次に
となり,絶対積分可能でない.次に
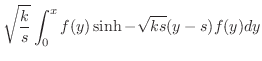 のフーリエ変換は
のフーリエ変換は
![$\displaystyle {\cal F}[f^{\prime}] = \int_{-\infty}^{\infty}f^{\prime}(x)e^{-i \omega x}dx. $](img2371.png)
 とおき,部分積分を用いると
とおき,部分積分を用いると
![$\displaystyle {\cal F}[f^{\prime}] = f(x)e^{-i \omega x}\mid_{\infty}^{\infty} ...
...infty}f(x)e^{-i \omega x}dx = (i \omega)F(\omega).
\ensuremath{ \blacksquare}
$](img2373.png)
ラプラス変換と同様,次のような微分法則が成り立ちます.
![$\displaystyle {\cal F}[f^{(n)}(x)] = (i \omega)^{n}F(\omega). $](img2374.png)
フーリエ変換 で,Eulerの公式
で,Eulerの公式
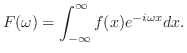 を用いると,
を用いると,
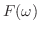 |
 |
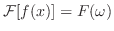 |
|
 |
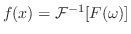 |
||
 |
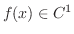 |
||
 |
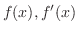 |
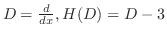 |
 |
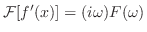 |
|
 |
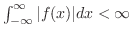 |
||
 |
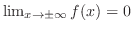 |
|
定理 8..2
 が が
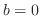 で区分的に滑らかで, で区分的に滑らかで,
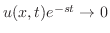 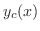 絶対積分可能 絶対積分可能 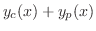 ならば ならば
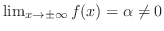
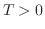
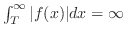
|
フーリエ余弦変換
 が
が
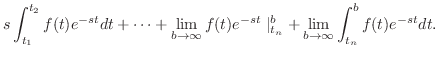 で区分的に滑らかで,
で区分的に滑らかで,
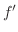
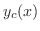 絶対積分可能
絶対積分可能 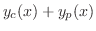 ならば
ならば
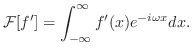 |
 |
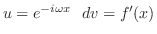 |
|
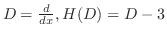 |
 |
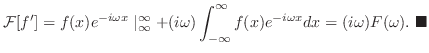 |
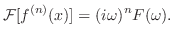 をフーリエ余弦変換(Fourier cosine transform) といいます.
をフーリエ余弦変換(Fourier cosine transform) といいます.
フーリエ正弦変換
 が
が
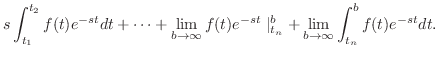 で区分的に滑らかで,
で区分的に滑らかで,
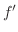
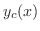 絶対積分可能
絶対積分可能 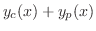 ならば
ならば
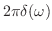 |
 |
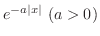 |
|
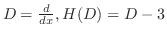 |
 |
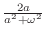 |
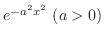 をフーリエ正弦変換(Fourier sine transform) といいます.
をフーリエ正弦変換(Fourier sine transform) といいます.
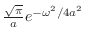
解
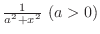
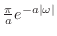 |
 |
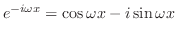 |
|
 |
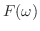 |
||
 |
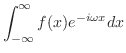 |
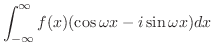 |
 |
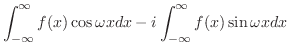 |
|
 |
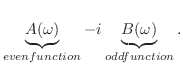 |
||
 |
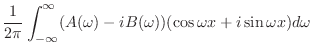 |
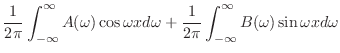

フーリエ変換の偏微分方程式への応用に行く前に.合成積のフーリエ変換について少し考えてみましょう.まず, と
と の合成積
の合成積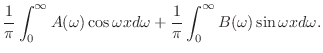 を
を
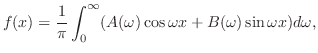
 が
が
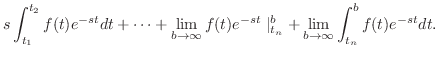 で絶対積分可能ならば次の定理が成り立ちます.
で絶対積分可能ならば次の定理が成り立ちます.
|
定理 8..3 (合成積のフーリエ変換)
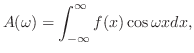
|
証明
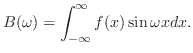 をそれぞれ
をそれぞれ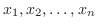 のフーリエ変換とすると,
のフーリエ変換とすると,
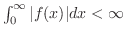
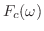
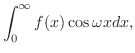 とおくと,
とおくと,
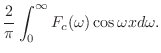 より
より
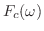 |
 |
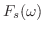 |
|
 |
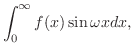 |
||
 |
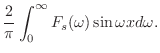 |
||
 |
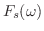 |