Next: フーリエ変換 Up: 3つの境界値問題(three boundary value problems) Previous: 熱伝導方程式(heat conduction equation) 目次 索引
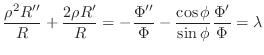
 のとき,両端が温度
のとき,両端が温度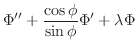 度の冷水の中につけられた.このとき棒の温度
度の冷水の中につけられた.このとき棒の温度 を求めよ.
を求めよ.
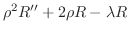 で与えられているときの温度
で与えられているときの温度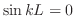 を求めよ.
を求めよ.
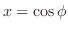 と
と
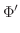 に保たれているとき,定常温度分布を求めよ.
に保たれているとき,定常温度分布を求めよ.
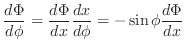 |
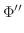 のとき のとき 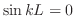 有界 有界 |
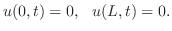 |
にラプラス変換を施し,
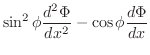 を仮定すると次の微分方程式を得ることを示せ.
を仮定すると次の微分方程式を得ることを示せ.
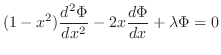
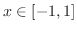 |
 |
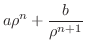 |
|
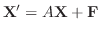 |
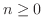 |
||
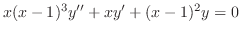 |
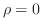 |